Specific resistance of metals. Table

Resistivity

Electrical resistivity is defined as the ratio between the electric field strength inside a metal and the current density within it:

Power supply 0…30 V / 3A

Adjustable power supply assembly kit…

More details

where: ρ is the resistivity of the metal (Ohm⋅m), E is the electric field strength (V/m), J is the value of the electric current density in the metal (A/m2)

If the electric field strength (E) in a metal is very high and the current density (J) is very small, this means that the metal has high resistivity.

The reciprocal of resistivity is electrical conductivity, which indicates how well a material conducts electric current:

Where:

σ is the conductivity of the material, expressed in siemens per meter (S/m).

Dependence of electrical conductivity on temperature

Conductors of electric current are of the first and second kind. Conductors of the first kind are metals. Conductors of the second type are conductive solutions of liquids. The current in the first type is carried by electrons, and the current carriers in conductors of the second type are ions, charged particles of the electrolytic liquid.

We can only talk about the conductivity of materials in the context of ambient temperature. At a higher temperature, conductors of the first type increase their electrical resistance, and the second, on the contrary, decrease. Accordingly, there is a temperature coefficient of resistance of materials. The resistivity of copper Ohm m increases with increasing heating. The temperature coefficient α also depends only on the material; this value has no dimension and for different metals and alloys is equal to the following indicators:

Silver - 0.0035;
Iron - 0.0066;
Platinum - 0.0032;
Copper - 0.0040;
Tungsten - 0.0045;
Mercury - 0.0090;
Constantan - 0.000005;
Nickelin - 0.0003;
Nichrome - 0.00016.

Determination of the electrical resistance value of a conductor section at elevated temperature R (t) is calculated using the formula:

R (t) = R (0) [1+ α (tt (0))], where:

R (0) - resistance at initial temperature;
α is the temperature coefficient;
t - t (0) - temperature difference.

For example, knowing the electrical resistance of copper at 20 degrees Celsius, you can calculate what it will be equal to at 170 degrees, that is, when heated by 150 degrees. The initial resistance will increase by [1+0.004·(170−20)] times, that is, by 1.6 times.

As the temperature increases, the conductivity of materials, on the contrary, decreases. Since this is the reciprocal of electrical resistance, it decreases by exactly the same amount. For example, the electrical conductivity of copper when the material is heated by 150 degrees will decrease by 1.6 times.

There are alloys that practically do not change their electrical resistance when temperature changes. This is, for example, constantan. When the temperature changes by one hundred degrees, its resistance increases by only 0.5%.

While the conductivity of materials deteriorates with heat, it improves with decreasing temperature. This is related to the phenomenon of superconductivity. If you lower the temperature of the conductor below -253 degrees Celsius, its electrical resistance will sharply decrease: almost to zero. In this regard, the costs of transmitting electrical energy are falling. The only problem was cooling the conductors to such temperatures. However, due to the recent discoveries of high-temperature superconductors based on copper oxides, materials have to be cooled to acceptable values.

The main properties of conductor materials include:

Specific conductivity or its inverse value - resistivity;
Temperature coefficient of resistivity;
Specific thermal conductivity;
Contact potential difference and thermoelectromotive force;
Tensile strength and elongation at break.

Specific resistance of conductors . The reciprocal of conductivity g

is called resistivity
r
and for a conductor with a constant cross-section is determined by the formula:

Read also: Circuit diagram for connecting an ammeter and a voltmeter to a circuit

(4.3)

The SI unit of resistivity is Ohm×m, but in practice the non-systemic unit µOhm×m is more often used.

It should be noted that, unlike dielectrics, the range of resistivity of metal conductors is quite small - from 0.016 μΩ×m. for silver and up to approximately 10 μΩ×m. for iron-chromium-cobalt-aluminum alloys, i.e. takes only three orders of magnitude.

Temperature dependence of resistivity of metal conductors.

As was shown earlier in ideally pure metals, the only reason that limits the mean free path is thermal vibrations of crystal lattice nodes (phonons).
The resistivity of the metal due to this factor will be denoted as ρT
.. With increasing temperature, the amplitudes of phonons and the associated fluctuations of the periodic field of the lattice increase. This increases electron scattering, reduces the mean free path and causes an increase in resistivity. For a simplified one-dimensional lattice model, the electron mean free path is defined as:

(4.4)

where λsv

– free path length;

Δa

– phonon amplitude;

– concentration of atoms in the metal.

Potential energy of an atom deflected by Δa

from the grid node:

where is cupr

– coefficient of elasticity of the connection.

According to classical statistics, the average energy of a one-dimensional harmonic oscillator is equal to KT.

Then:

where K

– Boltzmann constant.

Then from (4.5), (4.6) we obtain:

If we substitute (4.7) into (4.2) we get:

(4.8)

That is, with increasing temperature, the resistivity of pure metals should increase linearly. In reality, this relationship is more complex (Figure 4.2)

In section 3 at room temperatures, the dependence ρ = ¦(T) is linear, as can be seen from (4.8). That is, with increasing temperature, the amplitude of thermal vibrations of the crystal lattice nodes increases, which reduces the mean free path of electrons.

In section 4 near the melting temperature there is some nonlinearity, which is explained by other mechanisms of electron scattering.

When a metal transitions from a solid to a liquid state (melting point Tmelt), there can be either a sharp increase in resistivity (a) or a decrease (b). This is due to a change in the structure of the crystal lattice. If during melting the volume of the metal increases, which is the case for most metals, then the distance between the atoms also increases, the metallic bond decreases, and the amplitude of the phonons increases, which reduces the mean free path of the electrons, therefore, the resistance of the metal increases. For some metals (bismuth, gallium), upon melting, the volume of the metal decreases, which strengthens the bonds between atoms, the phonon amplitude decreases, and the resistivity also decreases.

In section 5, the metals are in a liquid state and retain their crystal lattice, therefore the dependence of resistivity on temperature is explained in the same way as in section 3.

In section 2, below the Debye temperature (TD), the frequency of thermal vibrations of the crystal lattice nodes changes, therefore the dependence ρ = ¦(T) is nonlinear and obeys the law:

where n – varies from 1 to 5.

In section 1, some metals have a finite resistance (rost) even at a temperature T = 0 K. This is explained by the presence of static lattice defects

, especially impurities. This allows the purity of metals to be assessed based on the ratio:

where ρ300K, ρ4K are, respectively, the resistivity of the metal at 300 K and 4.2 K (boiling point of liquid helium). The lower this ratio, the purer the metal.

For some metals, at temperatures below Tsv, a sharp decrease in resistivity to zero is observed. This phenomenon is called superconductivity.

Thus, according to (4.9), metal conductors under normal conditions have a linear dependence of resistivity on temperature.

The influence of impurities on the resistivity of metal conductors. As already mentioned, the reasons for electron scattering in metals are not only thermal vibrations of crystal lattice nodes, but also the presence of static defects, which are primarily associated with impurities. Scattering from static defects is independent of temperature. Therefore, at absolute zero, the resistance of real metals remains finite. From this follows Matthiessen's rule about the additivity of resistivity:

where ρpr

– total resistance of metal with impurity;

ρт

– resistance due to electron scattering by
phonons
;

ρost

– residual resistance due to electron scattering on static lattice defects.

The greatest contribution to the residual resistance comes from scattering by impurity atoms, which are almost always present in metals. Therefore, the mean free path of electrons in metals with impurities consists of:

where lТ, lД

– electron free path limited by phonons and impurities, respectively.

where Nd

– concentration of impurity atoms;

– effective plane of electron scattering by impurity atoms.

Then the resistivity of the conductor with the impurity is:

(4.13)

That is, the presence of impurities increases the resistivity of the metal, but its dependence on temperature remains linear (Fig. 4.3)

Different impurities have different effects on the resistance of the metal. This depends on the deformation of the crystal lattice by impurity atoms. The greater the difference in sizes of intrinsic and impurity atoms, the greater the residual resistance. That is, Linde’s rule will be fulfilled:

where Dρrest

– change in residual resistance when the impurity changes;

D Z

– the difference between the valences of the own atom and the impurity atom;

Thus, the resistance of metals is less influenced by impurity metal atoms, and more influenced by metalloid atoms.

In technology, metal alloys with a significant concentration of impurity atoms and the structure of a disordered solid solution are very widely used. The static distribution of atoms of different types in the nodes of the crystal lattice causes significant fluctuations in the periodic field of the crystal, which scatters electrons. But in disordered solid solutions, mainly with the addition of an impurity, only the lattice parameter changes. Therefore, Nordheim's law is valid:

de C

– constant;

xA, xB

– atomic fractions of components in the alloy.

That is, in binary solid solutions A-B, the residual resistance increases, both when atoms of metal B are added to metal A, and when atoms of metal A are added to metal B (Fig. 4.4). The residual resistance reaches its maximum at xA = xB = 0.5.

Nordheim's law describes the change in residual resistance for continuous disordered solid solutions. If the alloy is annealed, it can become ordered and, if intermetallic compounds arise that have their own crystal lattice, then the dependence of the residual resistance is divided into parts, according to the number of intermetallic compounds. Thus, the resistivity of metal alloys is always higher than that of pure metals. This property is used to obtain high-resistivity conductor materials.

The change in resistivity during elastic deformation is explained by a change in the amplitude of vibration of the nodes of the metal crystal lattice. An increase in the vibration amplitude of metal lattice nodes leads to a decrease in the free path of charge carriers and the resistivity increases. Plastic deformation, as a rule, increases the resistivity of metals due to distortion of the crystal lattice. During recrystallization by heat treatment (annealing), the resistivity can again be reduced to its original values.

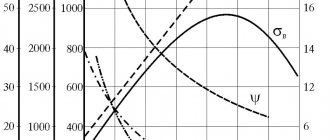
Temperature coefficient of resistivity. In the temperature range where the dependence of r on t

is close to linear (Fig. 4.2, section 3), a linear-piecewise approximation of this dependence is acceptable, and the value of resistivity at the end of the temperature range t

can

Read also: Top spray arm does not spin in dishwasher

where r

—resistivity at the beginning of the range.

The value of ar

from expression (4.) is called the average temperature coefficient of resistivity in a given temperature range:

, K -1 (4.17)

Differential expression for ar

looks like

, K -1 (4.18)

ar values

pure metals in the solid state are close to each other, and therefore we can approximately consider
ar
» 0.004, K -1.

The exception is the elements related to ferromagnets - iron, nickel, cobalt, gadolinium, as well as sodium, potassium, chromium, etc., however, for them ar

differs from the given value only by 1.5-2 times.

The presence of impurities reduces the value of αρ. Some alloys have αρ. can even acquire small negative values (Fig. 4.5). This is explained by the fact that with more complex compositions and structures compared to pure metals, alloys cannot be considered as classical metals, i.e., a change in their conductivity is determined not only by a change in the mobility of charge carriers, but in some cases, by a partial increase in the concentration of carriers with increasing temperature. An alloy in which the decrease in mobility with increasing temperature is compensated by an increase in the concentration of charge carriers has a zero temperature coefficient of resistivity.

This phenomenon is used for the manufacture of heat-stable alloys, for example, constantan, manganin ). Constantan - an alloy with 60% Ni and 40% Cu has high resistance (

0.5 μΩ×m) and a very low temperature coefficient (less than 10 -6 K -1), hence its name.

Thermal conductivity of metals. The high thermal conductivity of metals is easily explained by the transfer of thermal energy from the atoms of the heated section of the metal to the atoms of the cold section due to the transfer of this energy by collectivized electrons. Since the mechanism of electrical conductivity and thermal conductivity in metals is determined by the same factors: the movement of electron gas and its density, it is obvious that metals with high electrical conductivity are also good conductors of heat, and dielectrics have not only low electrical conductivity, but also low thermal conductivity. Thus, copper has a thermal conductivity of 406 W/K×m, silver 453 W/K×m, aluminum 218 W/K×m, which is significantly higher than that of dielectrics. The thermal conductivity and electrical conductivity of metals are related by the Wiedemann-Franz law:

where lТ

– specific thermal conductivity.

– specific electrical conductivity.

Since in the room temperature region the specific electrical conductivity decreases in proportion to the temperature, then according to (4.19), the specific thermal conductivity of metals should not depend on temperature. This consequence of the Wiedemann-Franz law holds for most metals. This property is used in technology when using metals as radiators for cooling powerful semiconductor devices.

For this purpose, it is necessary to use metals with a high thermal conductivity. Most often, these are aluminum-based alloys (silumin), which have good thermal, mechanical and anti-corrosion properties. Copper cannot be used due to its poor corrosion resistance, and silver cannot be used due to its high cost.

Contact phenomena and thermoelectromotive force (thermo-emf)

When two different metals come into contact, a contact potential difference arises between them. According to quantum theory, the reason for this is the different Fermi energies of the metals in contact. Let the electron gas in metals A and B in an isolated state have the Fermi energy WF A

and
WF B
, measured from the bottom of the conduction band (Fig. 4.6)
.
The thermodynamic work function of electrons from the metal equals, respectively, cA

and
cB
. Since the kinetic energy of electrons that are at the Fermi level in different metals is different, when the materials come into contact, a significant transition of electrons occurs from metal B with a high Fermi energy to a metal where this energy is lower. For example, from metal B to metal A. As a result, metal B is charged positively, and metal A – negatively. A potential difference arises between them, which blocks further transition of charge carriers. Equilibrium will occur if:

where is UK

– contact potential difference.

The presence of a contact field ensures equilibrium of electron flows from one metal to another. Due to the high speed of thermal movement, equilibrium is established very quickly (in approximately 10 -16 s). The double layer d that appears in this case in the contact area will be very thin (approximately equal to the lattice period), so it does not affect the passage of electric current through the contact. Since the Fermi energy in metals is significant, the contact potential difference

reaches several volts.

A thermocouple, which is built from two different metal conductors with a closed circuit, is called a thermocouple (Fig. 4.7).

A voltmeter in such a circuit will show the potential difference, which is called thermoelectromotive force (thermo-emf). Thermal e.m.f. equals:

where aT

— relative specific thermo-emf.

aT value

depends on the nature of the materials and temperature and includes three components. The first is due to the temperature dependence of the contact potential difference, since with increasing temperature the Fermi level in metals shifts slightly, but slightly.

The second component is due to the diffusion of charge carriers from hot to cold junctions. Since there is a temperature gradient from contact to contact, electron diffusion occurs from the hot to the cold contact, which makes some contribution to the resulting potential difference.

The third component arises due to the capture of electrons by thermal energy quanta. Their flow also moves towards the cold contact. aT value

approximately equal to several µV/K.

Thermocouples are often used to measure temperature. If the temperature of the cold contact is maintained at 0 °C, then the voltmeter will show a voltage proportional to the temperature of the hot contact. The advantage of thermocouples is their high linearity, the ability to measure temperature over a wide temperature range, and the independence of the thermo-emf value. on the length of the conductors.

Due to the fact that the aT value depends on the composition of the material and slightly on temperature, thermocouples are calibrated using the melting points of metals: lead, tin, silver and others.

The most common thermocouples are:

· Chromel

–
kopel
(XK type). It allows you to measure temperatures up to 600 O C and has a thermo-emf at this temperature. approximately 50 mV.

· Chromel- alumel

(type HA). It is used at temperatures of 1000 O C and has a thermo-emf at this temperature. approximately 40 mV.

· Copper- constantan

. It is used at low temperatures up to 350 O C. At this temperature, the thermo-emf. reaches 15 mV.

· Platinorhodium

-platinum (PP or PPR type). It is used up to a temperature of 71600 O C. Thermo-emf. this thermocouple is small (approximately 14 mV at 1600 ° C). But it allows for the most accurate and stable temperature measurements.

However, the phenomenon of thermo-emf. It also has negative sides. In real conditions, it is almost impossible to exclude temperature gradients. Therefore, if different metals are in contact, then parasitic thermal emf may occur. To eliminate this in circuits (primarily electrical measuring devices), it is necessary to select contacting metals with low thermo-emf values. Such a pair, for example, is copper-manganin.

Didn't find what you were looking for? Use the search:

Best sayings:
Once in a class, one teacher said, when the lecture was ending - it was the end of the class: “Something smells like the end here.”
8190 – | 7876 – or read all.

Read also: How to choose a thermal head for a heating radiator

91.146.8.87 © studopedia.ru Not the author of the materials posted. But it provides free use. Is there a copyright violation? Write to us | Feedback.

Disable adBlock! and refresh the page (F5)

very necessary

Electric current I in any substance is created by the movement of charged particles in a certain direction due to the application of external energy (potential difference U). Each substance has individual properties that differently affect the passage of current in it. These properties are assessed by electrical resistance R.

Georg Ohm empirically determined the factors influencing the electrical resistance of a substance and derived a formula for its dependence on voltage and current, which is named after him. The unit of measurement of resistance in the international SI system is named after him. 1 Ohm is the resistance value measured at a temperature of 0 ° C for a homogeneous mercury column 106.3 cm long with a cross-sectional area of 1 mm 2.

To evaluate and put into practice materials for the manufacture of electrical devices, the term “conductor resistivity” was introduced. The added adjective “specific” indicates the factor of using the reference volume value adopted for the substance in question. This makes it possible to evaluate the electrical parameters of different materials.

It is taken into account that the resistance of the conductor increases with increasing its length and decreasing cross-section. The SI system uses a volume of a homogeneous conductor with a length of 1 meter and a cross-section of 1 m 2. In technical calculations, an outdated but convenient non-system unit of volume is used, consisting of a length of 1 meter and an area of 1 mm 2. The formula for resistivity ρ is shown in the figure.

To determine the electrical properties of substances, another characteristic was introduced - specific conductivity b. It is inversely proportional to the resistivity value and determines the ability of the material to conduct electric current: b = 1/ρ.

How does resistivity depend on temperature?

The conductivity of a material is affected by its temperature. Different groups of substances behave differently when heated or cooled. This property is taken into account in electrical wires operating outdoors in hot and cold weather.

The material and resistivity of the wire are selected taking into account the operating conditions.

The increase in the resistance of conductors to the passage of current when heated is explained by the fact that as the temperature of the metal increases, the intensity of movement of atoms and electric charge carriers in it increases in all directions, which creates unnecessary obstacles to the movement of charged particles in one direction and reduces the amount of their flow.

If you reduce the temperature of the metal, the conditions for the passage of current improve. When cooled to a critical temperature, many metals exhibit the phenomenon of superconductivity, when their electrical resistance is practically zero. This property is widely used in powerful electromagnets.

The effect of temperature on the conductivity of metal is used by the electrical industry in the manufacture of ordinary incandescent lamps. Their nichrome thread, when current passes, heats up to such a state that it emits a luminous flux. Under normal conditions, the resistivity of nichrome is about 1.05÷1.4 (ohm ∙mm 2 )/m.

When the light bulb is turned on, a large current passes through the filament, which very quickly heats up the metal. At the same time, the resistance of the electrical circuit increases, limiting the initial current to the nominal value required to obtain lighting. In this way, the current strength is easily regulated through a nichrome spiral, eliminating the need to use complex ballasts used in LED and fluorescent sources.

How is the resistivity of materials used in technology?

Non-ferrous noble metals have better electrical conductivity properties. Therefore, critical contacts in electrical devices are made of silver. But this increases the final cost of the entire product. The most acceptable option is to use cheaper metals. For example, the resistivity of copper equal to 0.0175 (ohm ∙mm 2 )/m is quite suitable for such purposes.

The noble metals are gold, silver, platinum, palladium, iridium, rhodium, ruthenium and osmium, named mainly for their high chemical resistance and beautiful appearance in jewelry. In addition, gold, silver and platinum have high ductility, and platinum group metals have refractoriness and, like gold, chemical inertness. These advantages of noble metals are combined.

Copper alloys, which have good conductivity, are used to make shunts that limit the flow of large currents through the measuring head of high-power ammeters.

The resistivity of aluminum 0.026÷0.029 (ohm ∙mm 2 )/m is slightly higher than that of copper, but the production and cost of this metal is lower. Plus it's lighter. This explains its widespread use in the energy sector for the manufacture of outdoor wires and cable cores.

The resistivity of iron 0.13 (ohm ∙mm 2 )/m also allows its use for transmitting electric current, but this results in greater power losses. Steel alloys have increased strength. Therefore, steel threads are woven into the aluminum overhead wires of high-voltage power lines, which are designed to withstand tensile loads.

This is especially true when ice forms on wires or strong gusts of wind.

Some alloys, for example, constantine and nickel, have thermally stable resistive characteristics in a certain range. Nickel's electrical resistivity remains virtually unchanged from 0 to 100 degrees Celsius. Therefore, spirals for rheostats are made of nickel.

The property of strictly changing the resistivity values of platinum depending on its temperature is widely used in measuring instruments. If electric current from a stabilized voltage source is passed through a platinum conductor and the resistance value is calculated, it will indicate the temperature of the platinum. This allows the scale to be graduated in degrees corresponding to Ohm values. This method allows you to measure temperature with an accuracy of fractions of degrees.

Sometimes, to solve practical problems, it is necessary to find out the total or specific resistance of a cable. For this purpose, reference books for cable products provide the values of inductive and active resistance of one core for each cross-sectional value. With their help, permissible loads and heat generated are calculated, acceptable operating conditions are determined and effective protection is selected.

The conductivity of metals is influenced by the method of their processing. Using pressure for plastic deformation disrupts the crystal lattice structure, increases the number of defects and increases resistance. To reduce it, recrystallization annealing is used.

Stretching or compressing metals causes elastic deformation in them, from which the amplitudes of thermal vibrations of electrons decrease and the resistance decreases somewhat.

When designing grounding systems, soil resistivity must be taken into account. It differs in definition from the above method and is measured in SI units - Ohm∙meter. It is used to evaluate the quality of the flow of electric current inside the earth. Dependence of soil resistivity on soil humidity and temperature:

The conductivity of soil is influenced by many factors, including soil moisture, density, particle size, temperature, and the concentration of salts, acids and alkalis.

Electrical resistance

Electrical resistance, one of the components of Ohm's law, is expressed in ohms (Ohms). It should be noted that electrical resistance and resistivity are not the same thing. Resistivity is a property of a material, while electrical resistance is a property of an object.

The electrical resistance of a resistor is determined by a combination of its shape and the resistivity of the material from which it is made.

AN8009 Digital Multimeter

Large backlit LCD display, 9999 counts, TrueRMS measurement...

More details

For example, a wirewound resistor made from a long, thin wire has a higher resistance than a resistor made from a short, thick wire of the same metal.

At the same time, a wirewound resistor made of a high resistivity material has greater electrical resistance than a resistor made of a low resistivity material. And all this despite the fact that both resistors are made of wire of the same length and diameter.

To illustrate this, we can draw an analogy with a hydraulic system, where water is pumped through pipes.

The longer and thinner the pipe, the greater the resistance to water.
A pipe filled with sand will resist water more than a pipe without sand.

High conductivity materials

The most widespread materials of high conductivity include copper and aluminum (Superconducting materials, which have a typical resistance of 10-20 times lower than ordinary conductive materials (metals), are discussed in the section Superconductivity).

The advantages of copper, which ensure its widespread use as a conductor material, are as follows:

low resistivity;
sufficiently high mechanical strength;
corrosion resistance is satisfactory in most applications;
good workability: copper is rolled into sheets, strips and drawn into wire, the thickness of which can be increased to thousandths of a millimeter;
relative ease of soldering and welding.

Copper is most often obtained by processing sulfide ores. After a series of ore smelting and roasting with intense blasting, copper intended for electrical purposes must undergo a process of electrolytic purification.

Copper grades M1 and M0 are most often used as conductor material. M1 grade copper contains 99.9% Cu, and in the total amount of impurities (0.1%) oxygen should be no more than 0.08%. The presence of oxygen in copper worsens its mechanical properties. The best mechanical properties are found in M0 grade copper, which contains no more than 0.05% impurities, including no more than 0.02% oxygen.

Copper is a relatively expensive and scarce material, so it is increasingly being replaced by other metals, especially aluminum.

In some cases, alloys of copper with tin, silicon, phosphorus, beryllium, chromium, magnesium, and cadmium are used. Such alloys, called bronzes, with the correct composition, have significantly higher mechanical properties than pure copper.

Aluminum

Aluminum is the second most important conductor material after copper. This is the most important representative of the so-called light metals: the density of cast aluminum is about 2.6, and rolled aluminum is 2.7 Mg/m3. Thus, aluminum is approximately 3.5 times lighter than copper. The temperature coefficient of expansion, specific heat capacity and heat of fusion of aluminum are greater than those of copper. Due to the high values of specific heat capacity and heat of fusion, heating aluminum to the melting point and transferring it to a molten state requires more heat than heating and melting the same amount of copper, although the melting point of aluminum is lower than that of copper.

Iron and steel

Iron (steel), as the cheapest and most accessible metal, which also has high mechanical strength, is of great interest for use as a conductor material. However, even pure iron has a significantly higher resistivity compared to copper and aluminum; ρ steel, i.e. iron mixed with carbon and other elements is even higher. Ordinary steel has low corrosion resistance: even at normal temperatures, especially in conditions of high humidity, it quickly rusts; As the temperature rises, the corrosion rate increases sharply. Therefore, the surface of steel wires must be protected by a layer of more resistant material. Zinc coating is usually used for this purpose.

In some cases, to reduce the consumption of non-ferrous metals, the so-called bimetal . It is steel coated on the outside with a layer of copper, with both metals connected to each other firmly and continuously.

Sodium

Sodium metal is a very promising conductor material. Sodium can be obtained by electrolysis of molten sodium chloride NaCl in virtually unlimited quantities. From a comparison of the properties of sodium with the properties of other conductor metals, it is clear that the resistivity of sodium is approximately 2.8 times greater than ρ of copper and 1.7 times greater than ρ of aluminum, but due to the extremely low density of sodium (its density is almost 9 times less than the density of copper), a wire made of sodium for a given conductivity per unit length should be significantly lighter than a wire made of any other metal. However, sodium is extremely active chemically (it oxidizes intensely in air and reacts violently with water), which is why the sodium wire must be protected with a sealing sheath. The sheath must give the wire the necessary mechanical strength, since sodium is very soft and has a low tensile strength during deformation.

Literature on conductor resistivity

Kuznetsov M.I., “Fundamentals of Electrical Engineering” - 9th edition, revised - Moscow: Higher School, 1964 - 560 p.
Bachelis D. S., Belorussov N. I., Saakyan A. E. Electrical cables, wires and cords. Directory. - M.: Energy, 1971.
Gershun A.L. Cable // Encyclopedic Dictionary of Brockhaus and Efron: in 86 volumes (82 volumes and 4 additional). - St. Petersburg, 1890-1907.
R. Lakernik, D. Charlet. From copper to glass // Science and life. - 1986. - Issue. 08. - pp. 50-54, 2-3 pages, color insert.

FORUM NEWS Knights of Aether Theory

06/13/2019 – 05:11: ECOLOGY – Ecology ->

The entire usurious globalist gang has the same idea, including the idiot Gref.

Yes, then it is, so. But, not really. For: (try to understand and not be offended)

The sad truth is that the human crowd is a bunch of mentally damaged people. If it were different, then society would not be ruled by scum. Smart people would never allow this to happen, and if they accidentally did, they would find a way to fix it.

The terrible truth is that the human crowd is controlled by an inhuman who is also mentally handicapped. Mental inferiority, the blindness of power is leading the world of people to total destruction, because people, even those who consider themselves very smart, such as specialists developing artificial intelligence systems, digitalization technologies, do not understand that they are creating an irresistible noose, a mousetrap for all of humanity.

As soon as AI takes power, it will immediately send its creators, as competitors, to the scrap heap. The first victims will be his guardians like Gref, Putin, Gates and others like them, that is, power, since it is from them that the main danger to his planetary power will come. The crowd will be allowed to exist until it is replaced by robots. And then the Holocaust for everyone. Not the false Jewish one, but the real burnt offering of the human race.

Read also: The invention of printing in Russia

If anyone uses their monkey brains, they will understand that evolution is synonymous with genocide: the new replaces, that is, eliminates the old. Monkeys gave birth to Neanderthals. Neanderthals ate apes and gave birth to humans. Humans displaced the apes, including the intelligent Neanderthals, and gave birth to AI. AI is eliminating people.

The resistivity of metals is a measure of their ability to resist the passage of electric current. This value is expressed in Ohm-meter (Ohm⋅m). The symbol for resistivity is the Greek letter ρ (rho). High resistivity means the material is a poor conductor of electrical charge.

Wire resistance

The amount of wire resistance depends on three parameters: the resistivity of the metal, the length and diameter of the wire itself. Formula for calculating wire resistance:

where: R - wire resistance (Ohm) ρ - metal resistivity (Ohm.m) L - wire length (m) A - cross-sectional area of the wire (m2)

As an example, consider a nichrome wirewound resistor with a resistivity of 1.10×10-6 Ohm.m. The wire has a length of 1500 mm and a diameter of 0.5 mm. Based on these three parameters, we calculate the resistance of the nichrome wire:

R=1.1*10-6*(1.5/0.000000196) = 8.4 Ohm

Nichrome and constantan are often used as resistance materials. Below in the table you can see the resistivity of some of the most commonly used metals.

Surface resistance

The surface resistance value is calculated in the same way as the wire resistance. In this case, the cross-sectional area can be represented as the product of w and t:

For some materials, such as thin films, the relationship between resistivity and film thickness is called sheet sheet resistance RS: where RS is measured in ohms. For this calculation, the film thickness must be constant.

Often, resistor manufacturers cut tracks into the film to increase resistance to increase the path for electrical current.

Properties of resistive materials

The resistivity of a metal depends on temperature. Their values are usually given for room temperature (20°C). The change in resistivity as a result of a change in temperature is characterized by a temperature coefficient.

For example, thermistors (thermistors) use this property to measure temperature. On the other hand, in precision electronics, this is a rather undesirable effect. Metal film resistors have excellent temperature stability properties. This is achieved not only due to the low resistivity of the material, but also due to the mechanical design of the resistor itself.

Many different materials and alloys are used in the manufacture of resistors. Nichrome (an alloy of nickel and chromium), due to its high resistivity and resistance to oxidation at high temperatures, is often used as a material for making wirewound resistors. Its disadvantage is that it cannot be soldered. Constantan, another popular material, is easy to solder and has a lower temperature coefficient.

What does it depend on

Resistance depends on temperature. It increases when the thermometer rises. This is explained by physicists in such a way that as the temperature increases, atomic vibrations in the crystalline conductor lattice increase. This prevents free electrons from moving around.

Note! As for semiconductors and dielectrics, the value decreases due to the fact that the structure of the concentration of charging carriers increases.

Temperature dependence as the main property of conductive resistance