Why does a solid become liquid?
Heating a solid body leads to an increase in the kinetic energy of atoms and molecules, which at normal temperatures are located clearly at the nodes of the crystal lattice, which allows the body to maintain a constant shape and size. When certain critical speed values are reached, atoms and molecules begin to leave their places, bonds are broken, the body begins to lose its shape - it becomes liquid. The melting process does not occur abruptly, but gradually, so that for some time the solid and liquid components (phases) are in equilibrium. Melting refers to endothermic processes, that is, those that occur with the absorption of heat. The opposite process, when a liquid solidifies, is called crystallization.
Rice. 1. Transition of the solid, crystalline state of a substance into the liquid phase.
It was discovered that until the end of the melting process the temperature does not change, although heat is constantly supplied. There is no contradiction here, since the incoming energy during this period of time is spent on breaking the crystalline bonds of the lattice. After the destruction of all bonds, the influx of heat will increase the kinetic energy of the molecules, and consequently, the temperature will begin to rise.
Rice. 2. Graph of body temperature versus heating time.
General characteristics of lead
Lead is one of the most common metals on earth. It is widespread on the planet, in general, this explains its widespread use by humanity since ancient times. The metal has a high specific gravity, but at the same time it is quite soft and easy to process. The density of a metal depends on temperature; the higher the temperature, the lower the density. With a high specific density, it still remains soft, and it is easy to leave an impression on its surface even with a fingernail.
The metal does not have a very expressive appearance; when forged or milled, it quickly loses its shine due to the actively recovering oxide film on the surface. It belongs to the category of heavy metals. The specific density at room temperature of 20 degrees is 11.34 g/cm3.
A distinctive property of the metal is its low melting point. The fact is that, despite such a solid specific density and belonging to heavy metals, the melting point of lead is only 327.46 C. In addition, the addition of other refractory metals to the composition of lead does not ensure a change in its ductility.
Lead Ingots
Lead is absolutely unsuitable as a structural metal. The mechanical properties of the metal cannot boast of high performance:
- The hardness limit on the Brinell scale is 3.2-3.28 Nb;
- The ultimate strength in mechanical compression is achieved at a force of 50 MPa;
- The maximum tensile strength is only 13 MPa.
The metal also has low thermal conductivity, it is almost 2 times lower than that of iron and 11 times lower than that of copper - 33.5 W/(m*K). The heat capacity of the metal at 20 degrees is 0.128 kJ/(kg*K).
Lead is not the best conductor of electricity - the resistivity is 0.22 Ohm/mm2.
But regarding corrosion resistance, although it does not belong to noble metals, it is quite high. Lead in its pure form, without an oxide film, remains at a temperature of 850 degrees, so the protective oxide film on the metal acts as the main obstacle to corrosion.
Under normal conditions, the metal is practically invulnerable to ordinary sources of corrosion, but in dilute nitric acid with a concentration of less than 70% it is quickly destroyed. Although it is neutral to sulfurous, acetic, hydrofluoric and phosphoric acid. Another substance that destroys the oxide film on metal is sulfuric (90%) acid. When contacting other metals, the corrosion process begins under normal conditions, although such a reaction does not occur with iron and copper.
Determination of specific heat of fusion
The specific heat of fusion (designated by the Greek letter “lambda” - λ) is a physical quantity equal to the amount of heat (in joules) that must be transferred to a solid body weighing 1 kg in order to completely transform it into the liquid phase. The formula for the specific heat of fusion looks like this:
$$ λ ={Q \over m}$$
Where:
m is the mass of the melting substance;
Q is the amount of heat transferred to the substance during melting.
Values for different substances are determined experimentally.
Knowing λ, we can calculate the amount of heat that must be imparted to a body of mass m for its complete melting:
$$Q={λ*m}$$
Melting point prediction (Lindemann criterion)
An attempt to predict the melting point of crystalline materials was made in 1910 by Frederick Lindeman. The idea was the observation that the average amplitude of thermal fluctuations increases with increasing temperature. Melting begins when the vibration amplitude becomes large enough for neighboring atoms to partially occupy the same space.
Lindemann criterion
states that melting is expected when the rms value of the oscillation amplitude exceeds a threshold value.
The melting point of crystals is described quite well by the Lindemann formula:
Tλ=xm29ℏ2MkBθrs2{\displaystyle T_{\lambda }={\frac {x_{m}^{2}}{9\hbar ^{2}}}Mk_{B}\theta r_{s}^{2}}
where rs{\displaystyle r_{s}} is the average radius of the unit cell, θ{\displaystyle \theta } is the Debye temperature, and the parameter xm{\displaystyle x_{m}} for most materials varies in the range of 0.15-0, 3.
Melting point - Calculation
Lindemann's formula served as a theoretical basis for melting for almost a hundred years, but was not developed due to low accuracy.
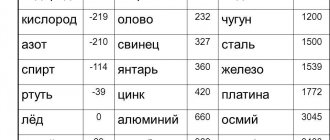
Specific heat of fusion of certain substances
Information on specific heat values for a specific substance can be found in book reference books or in electronic versions on Internet resources. They are usually presented in table form:
Specific heat of fusion of substances
| Substance | 105 * J/kg | kcal/kg | Substance | 105 * J/kg | kcal/kg |
| Aluminum | 3,8 | 92 | Mercury | 0,1 | 3,0 |
| Iron | 2,7 | 65 | Lead | 0,3 | 6,0 |
| Ice | 3,3 | 80 | Silver | 0,87 | 21 |
| Copper | 1,8 | 42 | Steel | 0,8 | 20 |
| Naphthalene | 1,5 | 36 | Zinc | 1,2 | 28 |
| Tin | 0,58 | 14 | Platinum | 1,01 | 24,1 |
| Paraffin | 1,5 | 35 | Gold | 0,66 | 15,8 |
One of the most refractory substances is tantalum carbide - TaC. It melts at a temperature of 39900C. TAC coatings are used to protect metal molds in which aluminum parts are cast.
Rice. 3. Metal melting process.
Notes
- S. T. Zhukov Chemistry 8-9 grades, Chapter 1. Basic ideas and concepts of chemistry
- The scatter of experimental data is apparently associated with the graphite-carbyne phase transition and different heating rates during measurements. Klimovsky I. I., Markovets V. V.
The influence of the graphite-carbyne phase transition on the emissivity of graphite samples when heated to temperatures of 3000 K or more // International Scientific Journal for Alternative Energy and Ecology. - 2007. - No. 6 (50). — P. 50-59. - Andreev V.D.
Selected problems of theoretical physics.. - Kiev: Avanpost-Prim. — 2012. - Meyer K. Physico-chemical crystallography, M., “Metallography”, 1972
- Lindemann FA // Phys.Z., 1910, v.11, p.609
- Wood WW, Jacobson JD
Preliminary Results from a Recalculation of the Monte Carlo Equation of State of Hard Spheres // J. Chem. Phys.. - 1957. - No. 27. - P. 1207. - DOI:10.1063/1.1743956. - Alder BJ, Wainwright TE
Phase Transition in Elastic Disks // Phys. Rev.. - 1962. - No. 127. - P. 359. - DOI:10.1103/PhysRev.127.359. - Hoover WG, Gray SG, Johnson KW
Thermodynamic Properties of the Fluid and Solid Phases for Inverse Power Potentials // J. Chem. Phys.. - 1971. - No. 55. - P. 1128. - DOI:10.1063/1.1676196. - Pines D. Elementary excitations in solids. M., Mir, 1965.
- Andreev V.D.
Crash - conformational kinematics of the covalent diamond lattice during melting. // Journal of structural chemistry. - 2001. - No. 3. - P. 486-495. - Andreev V.D.
“Factor of melting” during interatomic interactions in a diamond lattice. // Chemical physics. - 2002. - No. 8, t.21. — P. 35-40.
Properties of refractory metals and alloys
Examples
Crystallization is a very carefully studied process in chemistry, which is especially interesting in practice.
As an example, consider the process of sugar formation. The essence of the process is to isolate the sucrose contained in the syrup. The latter, in turn, also contains other substances that were not removed during the juice purification process, and were again formed during condensation.
When the temperature rises, crystallization begins, and in its process an intercrystalline solution is formed, which is called massecuite. All excess substances will accumulate in it. In fact, they seriously complicate the entire process, since the presence of various types of impurities increases the viscosity of the solution.
Another striking example of crystallization in chemistry is associated with the formation of salt. In order to see it with your own eyes, you don’t even need to conduct experiments - this process exists in nature. During the cold season, the surf throws tons of salt onto the shore. She doesn't disappear. It is raked into huge piles, and then, when it gets hot and dry, the water of crystallization evaporates from it. All that remains is fine powder—salt, consumed by industry.
The example with salt is the simplest. Even in some schools, children are given a homework assignment as part of a chemistry lesson: dissolve 1-2 tablespoons of salt in a very small amount of water and leave the container somewhere. For more intense crystallization, the temperature can be increased - move the solution closer to the battery, for example. In a couple of days the water will evaporate. But the salt crystals will remain.
Melting point prediction (Lindemann criterion)
An attempt to predict the melting point of crystalline materials was made in 1910 by Frederick Lindeman. The idea was the observation that the average amplitude of thermal fluctuations increases with increasing temperature. Melting begins when the vibration amplitude becomes large enough for neighboring atoms to partially occupy the same space.
Lindemann criterion
states that melting is expected when the rms value of the oscillation amplitude exceeds a threshold value.
The melting point of crystals is described quite well by the Lindemann formula:
Tλ=xm29ℏ2MkBθrs2{\displaystyle T_{\lambda }={\frac {x_{m}^{2}}{9\hbar ^{2}}}Mk_{B}\theta r_{s}^{2}}
where rs{\displaystyle r_{s}} is the average radius of the unit cell, θ{\displaystyle \theta } is the Debye temperature, and the parameter xm{\displaystyle x_{m}} for most materials varies in the range of 0.15-0, 3.
Melting point - Calculation
Lindemann's formula served as a theoretical basis for melting for almost a hundred years, but was not developed due to low accuracy.
In 1999 I.V. Gavrilin obtained a new expression for calculating the melting point:
Tm = DHm / 1.5 N k
, (1)
where Tpl
- melting temperature;
DHpl –
latent heat of fusion;
N
– latent heat of fusion;
k
– Boltzmann constant.
For the first time, an exceptionally compact expression (1) has been obtained for calculating the melting temperature of metals, connecting this temperature with known physical constants: latent heat of fusion, Avogadro's number and Boltzmann's constant.
The accuracy of calculations according to (1) can be assessed from the table data.
Table.
Melting point of some metals. Calculation by (1)
| Me | Al | V | Mn | Fe | Ni | Cu | Zn | Sn | Mo |
| DHpl kcal mol-1 | 2,5 | 5,51 | 3,5 | 4,4 | 4,18 | 3,12 | 1,7 | 1,7 | 8,7 |
| Tmel, K according to (1) | 876 | 1857 | 1179 | 1428 | 1406 | 1051 | 583 | 529 | 2945 |
| Tpl, K Exp. | 933 | 2190 | 1517 | 1811 | 1728 | 1357 | 692 | 505 | 2890 |
According to these data, the accuracy of Tmelt calculations varies from 2 to 30%, which is quite acceptable in calculations of this kind.
Formula (1) was derived as one of the consequences of the new theory of melting and crystallization, published in 2000.
— Gavrilin I.V. Melting and crystallization of metals and alloys. Ed. VlSU. Vladimir. 2000. 256 p.
Isothermal method and salting out
This should also be talked about. The isothermal crystallization process is characterized by the evaporation of water from solutions at a constant, unchanging temperature. This method is applicable for substances containing salts, the solubility of which is practically independent of heating.
Evaporation can be achieved by bringing the liquid to an intense boil and maintaining it in this state. This is the "traditional" method. Slow surface evaporation can also be used.
In some cases, substances are introduced into liquids that reduce their ability to dissolve. This is called salting out. Such “helpers” are substances that contain the same ion as the given salt. A striking example: the process of crystallization of sodium chloride from a solution with a high concentration to which magnesium chloride is added.
It should be noted that the salting out mechanism is not always the same. If, in order to carry out this process, you mix two electrolytes, the additional one of which will be with the same ion, then in the end you will achieve such a concentration that the solubility product of the substance will become significantly higher. What does it mean? In simple words, an excess of substance will appear and it will be released into the solid phase.
It happens differently. To achieve salting out, it is necessary to completely change the structure of the solution - to promote the formation of hydration shells around the particles of the substance that needs to be crystallized. How is this achieved? By destroying the shells of an already dissolved substance.
It is important to understand: salts that form crystalline hydrates are salted out more intensely than those that form in anhydrous form. But some “additives” only increase solubility
This leads to salting in.
Notes
- Dritsa M. E., Budberg P. B., Burkhanov G. S., Dritsa A. M., Panovko V. M.
Properties of elements. - Metallurgy, 1985. - P. 672. - ↑, p. 4.122.
- The melting point of purified water was measured to be 0.002519 ± 0.000002 °C, cm.
- Agte, C.;
Alterthum, H. Researches on Systems with Carbides at High Melting Point and Contributions to the Problem of Carbon Fusion (English) // Z. Tech. Phys. : journal. - 1930. - Vol. 11. - P. 182-191. - Lindemann FA (English)Russian.
The calculation of molecular vibration frequencies (German) // Phys. Z.: magazine. - 1910. - Bd. 11. - S. 609-612. - Zhirifalko L.
Statistical physics of solids. - M.: Mir, 1975. - P. 15. - Gavrilin I.V.
3.7. Calculation of the melting temperature of metals // Melting and crystallization of metals and alloys. — Vladimir: Publishing house. VlGU, 2000. - P. 72. - 200 copies. — ISBN 5-89368-175-4.