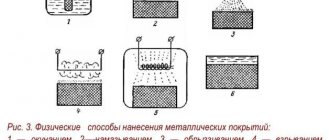
§ 26. General information
Bending is a method of processing metal by pressure, in which a workpiece or part thereof is given a curved shape. Bench bending is performed with hammers (preferably with soft strikers) in a vice, on a plate or using special devices. Thin sheet metal is bent with mallets, wire products with a diameter of up to 3 mm are bent with pliers or round nose pliers. Only plastic material is subject to bending.
Bending parts is one of the most common metalworking operations. The production of flexible parts is possible both manually using support tools and mandrels, and on bending machines (presses).
The essence of bending is that one part of the workpiece is bent relative to the other at a given angle. This happens in the following way: a bending force acts on a workpiece, freely lying on two supports, which causes bending stresses in the workpiece, and if these stresses do not exceed the elastic limit of the material, the deformation obtained by the workpiece is elastic, and upon removal of the load, the workpiece takes on its original view (straightens).
However, when bending, it is necessary to ensure that the workpiece, after removing the load, retains its given shape, therefore the bending stresses must exceed the elastic limit and the deformation of the workpiece in this case will be plastic, while the inner layers of the workpiece are subjected to compression and shortened, the outer layers are subject to tension and their length increases . At the same time, the middle layer of the workpiece - the neutral line - experiences neither compression nor tension, and its length before and after bending remains constant (Fig. 93a). Therefore, determining the dimensions of profile blanks comes down to calculating the length of straight sections (flanges), the length of shortening of the blank within the radius or the length of the neutral line within the radius.
When bending parts at right angles without rounding on the inside, the bend allowance is taken from 0.5 to 0.8 of the thickness of the material. By adding the length of the inner sides of the square or staple, we get the length of the workpiece.
Example 1
. In Fig. 93, c, d shows a square and a bracket with right internal angles.
Dimensions of the square (Fig. 93, c): a = 30 mm, b = 70 mm, t = 6 mm. Development length
L = a + b + 0.5t = 30 + 70 + 3 = 103 mm.
Bracket dimensions (Fig. 93, d): a = 70 mm, b = 80 mm, c = 60 mm, t = 4 mm. Reaming length of the staple blank
L = 70 + 80 + 60 + 2 = 212 mm.
We divide the square according to the drawing into sections. We substitute their dimensions a = 50 mm, b = 30 mm, t = 6 mm, r = 4 mm into the formula
L = a + b + π/2(r + t/2)
Then we get:
L = 50 + 30 + 3.14/2(4 + 6/2) = 50 + 30 + 1.57⋅7 = 90.99 91 mm.
We divide the bracket into sections, as shown in the drawing. Their dimensions: a = 80 mm, h = 65 mm, c = 120 mm, t = 5 mm, r = 2.5 mm.
L = a + h + c + π(r + t/2) = 80 + 65 + 120 + 3.14(2.5 + 5/2),
hence,
L = 265 4 + 15.75 = 280.75 mm.
By bending this strip into a circle, we obtain a cylindrical ring, with the outer part of the metal stretching somewhat and the inner part shrinking. Consequently, the length of the workpiece will correspond to the length of the center line of the circle, passing in the middle between the outer and inner circles of the ring.
Workpiece length
Knowing the diameter of the middle circumference of the ring and substituting its numerical value into the formula, we find the length of the workpiece:
L = πD = 3.14 108 = 339.12 mm.
As a result of preliminary calculations, it is possible to produce a part of the established dimensions.
During the bending process, significant stresses and deformations occur in the metal. They are especially noticeable when the bending radius is small. To prevent cracks from appearing in the outer layers, the bending radius should not be less than the minimum permissible radius, which is selected depending on the thickness and type of material being bent (Fig. 95).
The formula for the development length of a pipe blank helps to calculate the surface area or cross-section of a pipeline. The calculation is based on the size of the future route and the diameter of the planned structure. In what cases such calculations are required and how they are done, this article will tell you.
We give examples of calculations for manual and semi-automatic bending
The length of the workpiece is determined by the formula:
L = Y1 + X1 + ,
where Y1 and X1 are the length of straight sections of the sheet profile; φ – external angle; r – bending radius; K – neutral line position coefficient (determined from technical tables) S – metal thickness.
To determine the length of a workpiece with several bend angles, the amounts in parentheses for each additional angle are added to the above formula. The workpiece is calculated using the sweep method by summing the length of all straight flanges Yn, Xn and adding the curvature radius.
The force of the press on the workpiece when bending sheet metal is determined by the formula:
P = 1.42 × S2 × L × ∂ʋ/V
where S is the thickness of the metal sheet profile; L – workpiece length size; ∂ʋ – tensile strength (reference value); V – matrix scan (technical parameter of the machine).
In practice, experts use ready-made templates and tables depending on the type and size of the metal profile. The exact parameters of the workpiece are selected from the tables and the maximum permissible press forces with deformation angles are selected.
Calculations using formulas are used only when working with non-standard workpieces and single orders, where it is important to maintain dimensions exactly to 0.1 mm.
When are calculations needed?
Parameters are calculated using a calculator or using online programs
It is important to know what area the pipeline surface should have in the following cases.
- When calculating the heat transfer of a “warm” floor or register. Here the total area is calculated, which transfers heat emanating from the coolant to the room.
- When heat losses are determined along the way from a source of thermal energy to heating elements - radiators, convectors, etc. To determine the number and size of such devices, we need to know the amount of calories that we must have, and it is derived taking into account the development of the pipe.
- To determine the required amount of thermal insulation material, anti-corrosion coating and paint. When constructing highways that are kilometers long, accurate calculations save the enterprise considerable money.
- When determining a rationally justified profile section that could ensure maximum conductivity of the water supply or heating network.
Sheet metal bending has significant advantages compared to the welding process:
- after welding, the structure is often subjected to secondary processing, which ultimately increases the cost of the work done;
- after welding, there is a possibility that even the most highly qualified professional can make a mistake;
- the metal bending process is much cheaper than welding;
Thanks to the latest level of bending technology, more complex products can be manufactured. Sheet metal products are in demand in many areas. The absence of a seam resulting from welding is the main advantage of these products, which allows them to have reliability and higher strength.
An important point in this process is the calculation of sheet metal bending. All calculations are carried out near the intermediate line - these are the layers of the workpiece that do not change during the procedure. When the bending dimensions are not marked on the workpiece drawing, the master working with the bending machine independently determines them. Calculation of sheet metal bending is done in the middle of the workpiece, adding up the calculations of straight parts and curved zones. Machines for bending sheet metal (sheet benders) are divided into two types: manual and electric. The equipment for this process is distinguished by an almost identical principle - after fixing the workpiece with a pressure beam, it is bent to the required angle using a bending beam.
In the same way, the angle can be set on a press brake thanks to the punch and die. There are not very many types of punches - they usually differ in model and bending radii. The matrix, in most cases, is shaped like a groove or an angle of a given size.
The calculation method for bending sheet metal requires compliance with the following rules:
- if the workpiece has a hole, it is better that it is not located near the bend line, because there is a possibility that it may be pulled;
- The most suitable bending is along the grain of the metal sheet. As a result of exposure to high pressure along the bend line with a significant thickness of the sheet, the metal may burst;
- if it is not possible to use a rolling machine to produce a large radius bend, it is better to use a segment machine;
- when bending a metal sheet of considerable width on a press, a matrix imprint may subsequently remain on the product;
- Depending on the thickness of the metal, there is the smallest format of the sides allowed during bending. For example, for a sheet with a thickness of 1 mm, the smallest edge size is 10 mm, with a thickness of 2 mm, the smallest value is 12 mm, with a thickness over 3 mm - 15-20 mm, with a thickness of 10 mm - 50 mm.
The application of metal sheet bending is quite wide these days: the production of special elements in the field of construction, components of commercial equipment, beams, etc. In most cases, customers contact us when it is necessary to bend a significant amount of metal or in the absence of personal bending experience.
- Back
- Forward
Determination of pipe parameters
Cross-sectional area
The pipe is a cylinder, so calculations are not difficult
The cross-section of a round profile is a circle, the diameter of which is determined as the difference in the outer diameter of the product minus the wall thickness.
In geometry, the area of a circle is calculated as follows:
S = π R^2 or S= π (D/2-N)^2, where S is the internal cross-sectional area; π – number “pi”; R – section radius; D—outer diameter; N is the thickness of the pipe walls.
Note! If in pressure systems the liquid fills the entire volume of the pipeline, then in a gravity sewer only part of the walls is constantly wetted. In such collectors, the concept of open cross-sectional area of the pipe is used.
External surface
The surface of the cylinder, which is the round profile, is a rectangle. One side of the figure is the length of the pipeline section, and the second is the circumference of the cylinder.
Pipe development is calculated using the formula:
S = π DL, where S is the pipe area, L is the length of the product.
Inner surface
This indicator is used in the process of hydrodynamic calculations, when the surface area of the pipe that is constantly in contact with water is determined.
When determining this parameter, you should consider:
- The larger the diameter of the water pipes, the less the flow rate depends on the roughness of the walls of the structure.
On a note! If pipelines with a large diameter are characterized by a short length, then the value of the wall resistance can be neglected.
- In hydrodynamic calculations, the roughness of the wall surface is given no less importance than its area. If water flows through a water pipe that is rusty inside, then its speed is less than the speed of the liquid that flows through a relatively smooth polypropylene structure.
- Networks that are mounted from non-galvanized steel are characterized by a variable internal surface area. During operation, they become covered with rust and overgrown with mineral deposits, which narrows the lumen of the pipeline.
Important! Pay attention to this fact if you want to make cold water supply from steel material. The throughput of such a water supply system will be halved after ten years of operation.
The calculation of the pipe development in this case is made taking into account the fact that the internal diameter of the cylinder is determined as the difference between the external diameter of the profile and the double thickness of its walls.
As a result, the surface area of the cylinder is determined by the formula:
S= π (D-2N)L, where the indicator N is added to the already known parameters, which determines the wall thickness.
The workpiece development formula helps to calculate the amount of thermal insulation required
To know how to calculate the development of a pipe, it is enough to remember the geometry course that is taught in middle school. It’s nice that the school curriculum is used in adult life and helps solve serious problems related to construction. Let them be useful for you too!
As I promised in the comments to the article, today we’ll talk about calculating the length of the development of a part bent from sheet metal. Of course, not only sheet metal parts are subjected to the bending process. Bends parts of round and...
Square sections, bent and all rolled profiles - angles, channels, I-beams, pipes. However, cold bending of sheet metal parts is by far the most common.
To ensure minimum radii, parts are sometimes heated before bending. This increases the plasticity of the material. Using bending with a calibrating blow, it is ensured that the internal radius of the part becomes absolutely equal to the radius of the punch. With free V-shaped bending on a sheet bending machine, the internal radius in practice is greater than the radius of the punch. The more pronounced the spring properties of the part material are, the more different the internal radius of the part and the radius of the punch are from each other.
The figure below shows a bent sheet of thickness s
and width
b
corner. You need to find the sweep length.
Determining the development length when bending
Elements of the workpiece located in the deformable zone and adjacent to the inner surface of the bent part (from the punch side) are subject to compression, and those adjacent to the outer surface (from the matrix side) are subject to tension. Between the stretched and compressed fibers there is a neutral line whose length does not change (Drawing 106).
Crap. 106
The radius of the neutral line R in mm (drawing 106) is determined by the formula
R =r+ xs (46)
where r is the bending radius, mm;
s—material thickness mm;
x is a coefficient, the value of which depends on the ratio r/s (Table 48).
Table 48
| r/s ratio | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 1,0 | 1,2 |
| Coefficient x | 0,323 | 0,340 | 0,356 | 0,367 | 0,379 | 0,389 | 0,400 | 0,413 | 0,421 | 0,426 |
| r/s ratio | 1,5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 or more |
| Coefficient x | 0,441 | 0,445 | 0,463 | 0,469 | 0,477 | 0,780 | 0,485 | 0,490 | 0,495 | 0,500 |
When curling hinges (loops), due to the presence of external friction forces that prevent deformation, the coefficient x is determined from the table. 48a.
Table 48a
| r/s ratio | 1 | 1,2 | 1,4 | 1,6 | 1,8 | 2 | 2,2 |
| Coefficient x | 0,56 | 0,54 | 0,52 | 0,51 | 0,5 | 0,5 | 0,5 |
The development length of the bending part Lр in mm (Fig. 107) is determined by the formula
Lр=(l1+l2+l3+. . .)+ π/180(φ1R1+φ2R2+φ3R3+. . .) (47)
where l1; l2; l3—straight sections, mm;
φ1; φ2; φ3 — bending angles, degrees;
R1; R2; R3 are the radii of the neutral line, determined by formula (46).
Crap. 107
When bending materials over 3 mm thick at an angle of 90° with a bending radius r≤s, the radius of the neutral line R, calculated according to formula (46), must be adjusted to the value R1 (Fig. 108), based on the condition of material integrity and mating points a and a1 of a curved section of radius R1 with straight lines a-a and a1-a1 passing through the middle of the thickness s. In section C-C1, the dotted line shows the outer contour in the calculation without taking into account the thinning of the material. Due to thinning during bending, the thickness s1 in this area is less than the original s.
Crap. 108
The values R1 of the radius of the corrected neutral line and the length of the arc aba1 should be calculated using the formulas
(48)
(48a)
Where ;
R is determined by formula (46); r—bending radius, mm; other designations are shown in Fig. 108.
Elements for determining the dimensions of the reamers of commonly used bent parts are given in Table. 49.
Table 49
Note:
- y, y1, y2 are values that take into account the change in the development length when bending at an angle of 90°. For material thickness up to 2.5 mm, they are taken according to the table. 50, and with a thickness of 3 mm or more at r
- x - coefficient, taken according to the table. 48a.
Table 50
Table 50a
Example . Determine the length of the development for the part shown in Fig. 109.
Crap. 109
According to table.
49 Lр=l+l1+ у, where l and l1 are the lengths of the straight sections of the bent part;
y - find from the table. 50a
At s=4 mm and r= 3.5 mm
y=1.22 mm
Lp =50+40+ 1.22=91.22 mm.
If one-sided tolerances are specified in the working drawing of a part, then to calculate the length of the development, these tolerances must be recalculated to two-sided ones, while maintaining the specified tolerance field. In this case, the nominal dimensions of the part must also be recalculated (Fig. 110).
Crap. 110
In table 51 and 52 provide formulas for calculating the development length of bent parts with various initial data on the working drawing and various forms of mating.
Table 51
Note: x is the coefficient, determined from the table. 48.
Table 52
The dimensions of the developments of bent parts, calculated according to formula (47), should be clarified experimentally in the following cases:
- when two or more bending operations are combined in one die (Fig. 111 and 112,a).
- when bending ears, loops, etc. (Fig. 112,b);
- when the tolerances on the dimensions of bent parts are less than the tolerances of the 5th accuracy class.
The need to clarify the dimensions of the reamers is caused by the mixing of the neutral line during the bending process due to fluctuations in the mechanical properties of the material, different friction conditions on the contact surfaces of the material being processed and the working parts of the die, etc.
Crap. 111
Crap. 112
Related Pages
- Springback angles when bending
- Structural elements of working parts of bending dies
- Dies for bending complex parts (closed loop)
- Bending force calculation
- Reversal stamps
Related posts:
There are no similar entries.