Volume modulus of elasticity
(bulk modulus) is a characteristic of a substance’s ability to resist all-round compression.
This value determines how much external pressure needs to be applied to reduce the volume by 2 times K: Wikipedia: Articles without sources (type: not specified) [ source not specified 2012 days
]. For example, water has a volumetric modulus of elasticity of about 2000 MPa - this means that to reduce the volume of water by 1%, an external pressure of 20 MPa must be applied. On the other hand, with an increase in external pressure by 0.1 MPa, the volume of water decreases by 1/20000 part. The unit of measurement of the volumetric modulus of elasticity in the International System of Units (SI) is the pascal (Russian designation: Pa; international: Pa)[1].
Thermodynamic relations
Strictly speaking, the bulk modulus of elasticity is a thermodynamic quantity, and it is necessary to determine the bulk modulus of elasticity depending on the conditions of temperature change: at constant temperature (isothermal K_T), at constant entropy (adiabatic K_S), etc. In particular, such differences are usually important for gases.
In the case of an ideal gas, the isothermal and adiabatic moduli of volumetric elasticity are expressed by simple formulas. Thus, from the ideal gas isotherm equation p = \frac {\mathrm{const}}{V} it follows:
K_T=P\, .
Using the adiabatic equation p \, \cdot V^\gamma = \mathrm{const}, we can obtain
K_S=\gamma P,
where \gamma is the adiabatic exponent.
The given equations, which are satisfied exactly for ideal gases, become approximate when applied to real gases.
For liquids, the volumetric modulus of elasticity K
and density
ρ
determine the speed of sound
c
(pressure waves (
English
)), according to the Newton-Laplace formula
c=\sqrt{\frac{K}{\rho}}.
Volumetric compression ratio
Hydraulics. Hydrostatics
The main purpose of the collection is to provide students with material that will allow them to develop skills in applying theoretical information to solving specific technical problems and thereby master the practice of hydraulic calculations.
This course is the main theoretical discipline for specialties 2903, 2908, 2909, 1507, 1709.
This collection contains problems on hydrostatics and includes sections: “Physical properties of fluid”, “Hydrostatic pressure” and “Relative rest of fluid”.
Each section of the collection contains fairly complete information from the theory relating to the material in this section, methodological instructions and examples of solving some typical problems.
Four appendices provide reference materials that are necessary to solve problems.
The presence of extensive and varied material in the collection allows you to create an individual assignment for each student.
After familiarizing yourself with the relevant theoretical material and methodological instructions for solving typical problems, you should proceed to independently complete the assigned task.
Each task consists of several tasks, the numbers and options of which are given by the teacher. The task is carried out on A4 sheets, the necessary drawings are made in compliance with the selected scale.
PHYSICAL PROPERTIES OF LIQUIDS
Information from theory
A liquid is a physical body that has two distinctive features: a slight change in its volume under the influence of large external forces and fluidity, ease of movement, i.e. changing its shape under the influence of even minor external forces. One of the main mechanical characteristics of a liquid is density.
Density.
Density r (kg/m3) is the mass of a unit volume of liquid:
, (1.1)
where m –
liquid body mass, kg;
W
– volume, m3.
The density of liquids decreases with increasing temperature. The exception is water in the temperature range from 0 to 4 0 C, when its density increases, reaching its highest value at a temperature of 4 0 C r =
1000 kg/m3.
Specific gravity
The specific gravity g (N/m 3 ) of a liquid is the weight of a unit volume of this liquid:
, (1.2)
where G
– weight of the liquid body, N;
W
– volume, m3.
For water at a temperature of 4 0 C g =
9810 N/m 3.
There is a relationship between density and specific gravity:
, (1.3)
where g
– free fall acceleration equal to 9.81 m/s 2 .
The resistance of liquids to changes in their volume under the influence of pressure and temperature is characterized by the coefficients of volumetric compression and thermal expansion.
Volumetric compression ratio
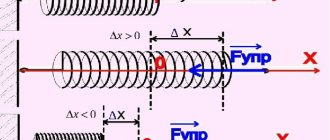
The volumetric compression coefficient bw (Pa -1) is the relative change in the volume of liquid when the pressure changes by unit:
, (1.4)
where D W
– change in volume
W
;
D r – change in density r, corresponding to a change in pressure by the amount D p
.
The reciprocal of the volumetric compression ratio is called the modulus of elasticity of liquids Ezh
(Pa)
. (1.5)
The value of the modulus of elasticity of liquids depends on pressure and temperature. If we assume that the pressure increment is , and the volume change is:
; (1.6)
. (1.7)
1.1.4. Thermal expansion coefficient
- The coefficient of thermal expansion b t
( 0 C) -1, expresses the relative change in the volume of liquid with a change in temperature by one degree:
, (1.8)
where D W
– change in volume
W
corresponding to a change in temperature by the amount D
t
.
The coefficient of thermal expansion of water increases with increasing temperature and pressure; for most other dripping liquids b t
decreases with increasing pressure.
If we accept that the temperature increase D t
=
t – t
0, and the volume change
; (1.9)
. (1.10)
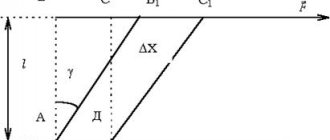
Viscosity is the property of a liquid to resist the movement of one part of the liquid relative to another. Viscosity appears only when the fluid moves and affects the distribution of velocities over the live cross section of the flow (Fig. 1.1).
According to Newton's hypothesis, the internal friction force F
in liquids it is proportional to the gradient of the change in speed, the contact area of the layers
S
, depends on the type of liquid and very slightly depends on pressure.
, (1.11)
where S –
area of contacting layers, m 2 ;
du –
displacement speed of layer “
b
” relative to layer “
a
”, m/s;
dy is
the distance at which the speed of movement of the layers changed by
du
, m;
–
velocity gradient, change in velocity normal to the direction of movement (s -1); m is the coefficient of dynamic viscosity (Pa s).
If the friction force F
referred to the unit area of the contacting layers, we obtain the value of the tangential stress t, and then (1.11) will take the form:
. (1.12)
From (1.12) it follows that the coefficient of dynamic viscosity can be defined as:
. (1.13)
From (1.13) it is easy to establish the physical meaning of the coefficient of dynamic viscosity. With a speed gradient =
1
;
m = t and expresses the force of internal friction per unit surface area of the contacting layers of liquid.
In practice, to characterize the viscosity of a liquid, it is often not the dynamic viscosity coefficient that is used, but the kinematic viscosity coefficient n (m 2 /s). The coefficient of kinematic viscosity is the ratio of the coefficient of dynamic viscosity to the density of the liquid:
. (1.14)
The viscosity of a liquid depends on the type of liquid, temperature and pressure.
Dependence of the viscosity of mineral oils used in hydraulic systems on pressure p
when it increases to 50 MPa, it can be determined using an approximate empirical formula:
, (1.15)
where n p
and
n
– kinematic viscosity, respectively, at pressure
p
and 0.1 MPa;
K
– experimental coefficient, depending on the brand of oil: for light oils (n 50 -6 m 2
/
s)
K =
0.02, for heavy oils (n
50
> 15 10 -6 m 2
/
s)
K =
0.03 . At low pressures, the change in viscosity is neglected. As the temperature increases, the viscosity of the liquid decreases. The dependence of the kinematic viscosity coefficient on temperature is determined by the empirical formula:
.
(1.16)
For lubricating oils used in machines and hydraulic systems, the following relationship is recommended:
, (1.17)
where nt is kinematic viscosity at temperature t; n 50 –
kinematic viscosity at a temperature of 50
0
C;
n
– exponent depending on n 50, determined by the formula:
. (1.18)
The viscosity of the liquid is determined using an Engler viscometer and is expressed in degrees Engler (0 E). The Angler degree (0 E) is the ratio of the flow time of the test liquid to the flow time of distilled water. To transfer from viscosity in degrees Engler to the kinematic viscosity coefficient n, the Ubellode formula is used:
. (1.19)
Viscosity is also determined using an Ostwald capillary viscometer. The coefficient of kinematic viscosity in this case is determined by the formula:
, (1.20)
where with
– device constant;
Tf
– liquid flow time, s.
Date added: 2015-12-08; ; ORDER A WORK WRITING
Some meanings
Approximate values of the bulk modulus of elasticity (K) for some materials
| Material | Bulk modulus of elasticity in GPa | Volumetric modulus of elasticity in lbf per square inch |
| Glass (see also diagram below table) | from 35 to 55 | 5,8×103 |
| Steel | 160 | 23×103 |
| Diamond[2] | 442 | 64×103 |
Approximate values of the bulk modulus of elasticity (K) for other substances
| Water | 2.2×109 Pa (value increases at higher pressures) |
| Air | 1.42×105 Pa (Adiabatic bulk modulus of elasticity) |
| Air | 1.01×105 Pa (volumetric modulus of elasticity at constant temperature) |
| Solid helium | 5×107 Pa (approx.) |
Physical properties of liquids
Chapter 1. BASICS OF HYDROSTATICS
The main physical properties of a liquid are: fluidity, density, specific gravity, viscosity, compressibility, thermal expansion.
The density of a liquid is a physical quantity numerically equal to the ratio of the mass of a liquid to its volume.
(1.1)
where r
– liquid density,
kg
/
m3
;
m
– mass of liquid;
kg
;
W
– volume of liquid,
m3
.
Specific gravity is a physical quantity numerically equal to the ratio of the weight of a liquid to its volume.
(1.2)
where g
– specific gravity of the liquid,
N
/
m3
;
Between specific gravity g
and density
r
there is a dependence
(1.3
where g
= 9.81
m
/
s
2 – free fall acceleration.
r values
and
g
for water and some other liquids at different temperatures are given in Appendix 1.
Viscosity is the property of a liquid to resist relative shear of adjacent layers. Viscosity is characterized by dynamic viscosity coefficients m
,
Pa×s
, and
kinematic viscosity n
,
m
/
s
. There is a relationship between these coefficients
(1.4)
The values of the coefficients of dynamic and kinematic viscosity for some liquids are given in Appendix 2.
Compressibility is the property of a liquid to change its volume when pressure changes. Compressibility is characterized by the volumetric compression ratio b
w, which can be determined by the formula
(1.5)
where b
w – volumetric compression ratio, 1/
Pa
;
W
– initial volume of liquid,
m3
;
D W
– change in liquid volume,
m3
;
D p
– change in pressure,
Pa
.
The reciprocal of the volumetric compression ratio is called the volumetric modulus of elasticity K
.
The bulk modulus is measured in Pa
.
(1.6)
The volumetric compression coefficients of liquids change little with changes in temperature and pressure. The values of volumetric compression coefficients and elastic moduli for some liquids are given in Appendix 3.
Thermal expansion is the property of a liquid to change its volume when the temperature changes. Thermal expansion is characterized by the coefficient of thermal expansion , which can be determined from the expression
(1.7)
where is the coefficient of thermal expansion, 1/ K
;
W
– initial volume of liquid,
m3
;
– change in liquid volume, m
3 ;
– temperature change, K
.
Thermal expansion coefficients for some liquids are given in Appendix 4.
Tasks
1.1. Determine the mass of water in a sleeve with a diameter of 51 mm
and 20
m long.
Solution. The mass of water is determined from formula (1.1)
Density of water according to Appendix 1
1.2. Determine the weight of water in hoses with a diameter of 66 mm
and 77
mm
and length 20
m
.
1.3. Determine the mass of diesel fuel oil contained in a tank with a volume of 50 m3
3 if the density of fuel oil is 920
kg
/
m3
.
1.4. Determine how much volume oil with a mass of 20×10 3 kg
and density 900
kg
/
m3
.
1.5. Determine the density of petroleum products if their mass is 17.5 × 10 3 kg
, volume 20
m3
.
1.6. Determine the weight of ethyl alcohol in a volume of 20 liters.
1.7. Fuel oil level in a vertical cylindrical tank with a diameter of 2 m
dropped by 0.5
m
.
Determine the mass of consumed fuel oil if its density at a temperature of 20 ° C
is 990
kg
/
m3
.
1.8. During hydraulic tests, water leakage is allowed, which should not exceed 3 liters
per square meter of wetted surface.
Is it possible to put into operation a rectangular reservoir with dimensions in plan of 12´6 m
m
to 3.48
m
in one day ? Determine the mass of lost water.
Solution . The volume of lost water was
Mass of lost water
Wetted surface area
Water leakage from one square meter of wetted surface during hydraulic tests
which exceeds the established norm.
1.9. Determine whether it is possible to put into operation a cylindrical tank with a diameter of 12 m
, in which the water level dropped from 5
m
to 4.985
m
.
1.10. Determine the maximum mass of water lost in one day as a result of hydraulic tests of a cylindrical tank with a diameter of 18 m
.
Determine the maximum reduction in water level if the initial level was 3.9 m
.
1.11. Determine the coefficient of dynamic viscosity of oil if the coefficient of kinematic viscosity is 0.624×10 -4 m
2/
s
.
Oil density is 750 kg
/
m3
.
1.12. Fire water conduit with a diameter of 300 mm
and 50
m
, prepared for hydraulic tests, filled with water at atmospheric pressure.
Determine the volume of water that needs to be additionally supplied to the water pipeline so that the excess pressure in it rises to 5 MPa
. Neglect the deformation of the water supply pipes.
Solution . From equation (1.5) we find that the volume of water that needs to be additionally supplied to the water pipeline is determined as
Volumetric compression ratio of water
Initial volume of water
1.13. During hydraulic testing of a process pipeline 200 m
and with a diameter of 250
mm
, filled with kerosene, the pressure was raised to 1.5
MPa
.
After one hour, the pressure dropped to 1.0 MPa
.
Determine the volume of kerosene leaked through the leak. Take the volumetric compression ratio of kerosene = 80×10 -11 1/ Pa
. Neglect pipeline deformation.
1.14. The pressure gauge on a process tank completely filled with oil shows 0.5 MPa
.
When 40 liters
of oil were released, the pressure gauge readings dropped to 0.1
MPa
. Determine the volume of the container if the volumetric compression ratio of oil = 80×10 -11 1/Pa.
1.15. In a vertical cylindrical tank with a diameter of 5 m
there is 1.2×10 5
kg
of oil, the density of which at 0 °
C
is 800
kg
/
m
3.
Determine fluctuations in the oil level in the tank when the temperature changes from 0 °
C to
30 °
C.
1.16. Determine fluctuations in the water level in the tank of a water tower when the temperature changes from 10 ° C
up
to 35 °
C. A water tank with a diameter of 3 m
contains 20
m
3 of water.
Take the coefficient of thermal expansion of water equal to 2×10 -4 1
/ K.
1.17. Maximum height of benzene level in a vertical cylindrical tank with a diameter of 12 m
equal to 10
m
at a temperature of 10
°
C. Determine to what level it is possible to pour benzene with a possible increase in temperature to 30
° C. Neglect expansion of the reservoir.
Didn't find what you were looking for? Use the search:
Best sayings:
What kind of mathematicians are you if you can’t password protect properly.
8406 – | 7319 – or read all.
193.151.241.65 © studopedia.ru Not the author of the materials posted. But it provides free use. Is there a copyright violation? Write to us | Feedback.
Disable adBlock! and refresh the page (F5)
very necessary
Notes
- [hyperphysics.phy-astr.gsu.edu/hbase/permot3.html Bulk Elastic Properties]. hyperphysics
. Georgia State University. [www.webcitation.org/6AIhR7XkB Archived from the original on August 30, 2012]. - (1985) “Calculation of bulk moduli of diamond and zinc-blend solids.” Phys. Rev. B 32
:7988–7991. DOI:10.1103/PhysRevB.32.7988. Bibcode: [adsabs.harvard.edu/abs/1985PhRvB..32.7988C 1985PhRvB..32.7988C]. - Fluegel, Alexander
[www.glassproperties.com/bulk_modulus/ Bulk modulus calculation of glasses].
glassproperties.com
. [www.webcitation.org/6AIhRZh2a Archived from the original on August 30, 2012].
| p • o • p Elastic moduli for homogeneous isotropic materials |
| Bulk modulus (K) | Young's modulus (E) | Lame parameters (\lambda) | Shear modulus (G) | Poisson's ratio (\nu) | en:P-wave modulus (M) |
An excerpt characterizing the Bulk Modulus of Elasticity
“If anyone else bothers me,” he said, rarely letting words slip through his clenched and thin lips, “I’ll bring him down here now.” Well!... Saying “well”!, he turned around again, let go of his hands, took the bottle and brought it to his mouth, threw his head back and threw his free hand up for leverage. One of the footmen, who began to pick up the glass, stopped in a bent position, not taking his eyes off the window and Dolokhov’s back. Anatole stood straight, eyes open. The Englishman, his lips thrust forward, looked from the side. The one who stopped him ran to the corner of the room and lay down on the sofa facing the wall. Pierre covered his face, and a weak smile, forgotten, remained on his face, although it now expressed horror and fear. Everyone was silent. Pierre took his hands away from his eyes: Dolokhov was still sitting in the same position, only his head was bent back, so that the curly hair of the back of his head touched the collar of his shirt, and the hand with the bottle rose higher and higher, shuddering and making an effort. The bottle was apparently emptied and at the same time rose, bending its head. “What’s taking so long?” thought Pierre. It seemed to him that more than half an hour had passed. Suddenly Dolokhov made a backward movement with his back, and his hand trembled nervously; this shudder was enough to move the entire body sitting on the sloping slope. He shifted all over, and his hand and head trembled even more, making an effort. One hand rose to grab the window sill, but dropped again. Pierre closed his eyes again and told himself that he would never open them. Suddenly he felt that everything around him was moving. He looked: Dolokhov was standing on the windowsill, his face was pale and cheerful. - Empty! He threw the bottle to the Englishman, who deftly caught it. Dolokhov jumped from the window. He smelled strongly of rum. - Great! Well done! So bet! Damn you completely! - they shouted from different sides. The Englishman took out his wallet and counted out the money. Dolokhov frowned and was silent. Pierre jumped onto the window. Gentlemen! Who wants to bet with me? “I’ll do the same,” he suddenly shouted. “And there’s no need for a bet, that’s what.” They told me to give him a bottle. I'll do it... tell me to give it. - Let it go, let it go! – said Dolokhov, smiling. - What you? crazy? Who will let you in? “Your head is spinning even on the stairs,” they spoke from different sides. - I'll drink it, give me a bottle of rum! - Pierre shouted, hitting the table with a decisive and drunken gesture, and climbed out the window. They grabbed him by the arms; but he was so strong that he pushed the one who approached him far away. “No, you can’t persuade him like that,” said Anatole, “wait, I’ll deceive him.” Look, I bet you, but tomorrow, and now we're all going to hell. “We’re going,” Pierre shouted, “we’re going!... And we’re taking Mishka with us... And he grabbed the bear, and, hugging and lifting him, began to spin around the room with him. Prince Vasily fulfilled the promise made at the evening at Anna Pavlovna's to Princess Drubetskaya, who asked him about her only son Boris. He was reported to the sovereign, and, unlike others, he was transferred to the Semenovsky Guard Regiment as an ensign. But Boris was never appointed as an adjutant or under Kutuzov, despite all the efforts and machinations of Anna Mikhailovna. Soon after Anna Pavlovna's evening, Anna Mikhailovna returned to Moscow, straight to her rich relatives Rostov, with whom she stayed in Moscow and with whom her beloved Borenka, who had just been promoted to the army and was immediately transferred to guards ensigns, had been raised and lived for years since childhood. The Guard had already left St. Petersburg on August 10, and the son, who remained in Moscow for uniforms, was supposed to catch up with her on the road to Radzivilov. The Rostovs had a birthday girl, Natalya, a mother and a younger daughter. In the morning, without ceasing, trains drove up and drove off, bringing congratulators to the large, well-known house of Countess Rostova on Povarskaya throughout Moscow. The countess with her beautiful eldest daughter and guests, who never ceased replacing one another, were sitting in the living room.