Объёмный мо́дуль упру́гости
(модуль объёмного сжатия) — характеристика способности вещества сопротивляться всестороннему сжатию. Эта величина определяет, какое нужно приложить внешнее давление для уменьшения объёма в 2 раза К:Википедия:Статьи без источников (тип: не указан)[
источник не указан 2012 дней
]. Например, у воды объёмный модуль упругости составляет около 2000 МПа — это означает, что для уменьшения объёма воды на 1 % необходимо приложить внешнее давление 20 МПа. С другой стороны, при увеличении внешнего давления на 0,1 МПа объём воды уменьшается на 1/20000 часть. Единицей измерения объёмного модуля упругости в Международной системе единиц (СИ) является паскаль (русское обозначение: Па; международное: Pa)[1].
Термодинамические соотношения
Строго говоря, объёмный модуль упругости является термодинамической величиной, и необходимо определить объёмный модуль упругости в зависимости от условий изменения температуры: при постоянной температуре (изотермический K_T), при постоянной энтропии (адиабатический K_S) и т. д. В частности, подобные различия обычно важны для газов.
В случае идеального газа изотермический и адиабатический модули объёмной упругости выражаются простыми формулами. Так, из уравнения изотермы идеального газа p = \frac {\mathrm{const}}{V} следует:
K_T=P\, .
Используя уравнение адиабаты p \, \cdot V^\gamma = \mathrm{const}, можно получить
K_S=\gamma P,
где \gamma — показатель адиабаты.
Приведённые уравнения, выполняющиеся точно для идеальных газов, применительно к реальным газам становятся приближёнными.
Для жидкостей объёмный модуль упругости K
и плотность
ρ
определяют скорость звука
c
(волны давления (
англ.
)), согласно формуле Ньютона-Лапласа
c=\sqrt{\frac{K}{\rho}}.
Коэффициент объемного сжатия
Гидравлика. Гидростатика
Основное назначение сборника – дать студентам материал, который позволит выработать навыки применения теоретических сведений к решению конкретных задач технического характера и тем самым освоить практику гидравлических расчётов.
Данный курс является основной теоретической дисциплиной для специальностей 2903, 2908, 2909, 1507, 1709.
Данный сборник содержит задачи по гидростатике и включает разделы: “Физические свойства жидкости”, “Гидростатическое давление” и “Относительный покой жидкости”.
Каждый раздел сборника содержит достаточно полные сведения из теории, касающейся материала данного раздела, методические указания и примеры решения некоторых типовых задач.
В четырёх приложениях даются материалы справочного характера, которые необходимы для решения задач.
Наличие в сборнике обширного и разнообразного материала позволяет составить индивидуальное задание для каждого студента.
После ознакомления с соответствующим теоретическим материалом и методическими указаниями по решению типовых задач, следует переходить к самостоятельному выполнению полученного задания.
Каждое задание состоит из нескольких задач, номера и варианты которых выдаются преподавателем. Задание выполняется на листах формата А4, необходимые чертежи выполняются с соблюдением выбранного масштаба.
ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
Сведения из теории
Жидкостью называется физическое тело, обладающее двумя отличительными особенностями: незначительным изменением своего объема под действием больших внешних сил и текучестью, легкоподвижностью, т.е. изменением своей формы под действием даже незначительных внешних сил. Одной из основных механических характеристик жидкости является плотность.
Плотность.
Плотностью r (кг/м 3 ) называется масса единицы объема жидкости:
, (1.1)
где m –
масса жидкого тела, кг;
W
– объем, м 3 .
Плотность жидкостей уменьшается с увеличением температуры. Исключение представляет вода в диапазоне температур от 0 до 4 0 С, когда ее плотность увеличивается, достигая наибольшего значения при температуре 4 0 С r =
1000 кг/м 3 .
Удельный вес
Удельным весом g (Н/м 3 ) жидкости называется вес единицы объема этой жидкости:
, (1.2)
где G
– вес жидкого тела, Н;
W
– объем, м 3 .
Для воды при температуре 4 0 С g =
9810 Н/м 3 .
Между плотностью и удельным весом существует связь:
, (1.3)
где g
– ускорение свободного падения, равное 9,81 м/с 2 .
Сопротивление жидкостей изменению своего объема под действием давления и температуры характеризуется коэффициентами объемного сжатия и температурного расширения.
Коэффициент объемного сжатия
Коэффициент объемного сжатия b w (Па -1 ) – это относительное изменение объема жидкости при изменении давления на единицу:
, (1.4)
где D W
– изменение объема
W
; D r – изменение плотности r , соответствующие изменению давления на величину D
p
.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкостей Eж
(Па)
. (1.5)
Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления , а изменение объема то:
; (1.6)
. (1.7)
1.1.4. Коэффициент температурного расширения
- Коэффициент температурного расширения b t
( 0 С) -1 , выражает относительное изменение объема жидкости при изменении температуры на один градус:
, (1.8)
где D W
– изменение объема
W
, соответствующее изменению температуры на величину D
t
.
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей b t
с увеличением давления уменьшается. Если принять, что приращение температуры D
t
=
t – t
0, а изменение объема
; (1.9)
. (1.10)
Вязкостью называется свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой. Вязкость проявляется только при движении жидкости и сказывается на распределении скоростей по живому сечению потока (рис. 1.1).
Согласно гипотезе Ньютона сила внутреннего трения F
в жидкостях пропорциональна градиенту изменения скорости , площади соприкосновенияслоев
S
, зависит от рода жидкости и очень незначительно зависит от давления.
, (1.11)
где S –
площадь соприкасающихся слоев, м 2 ;
du –
скорость смещения слоя “
b
” относительно слоя “
a
“, м/с;
dy –
расстояние, на котором скорость движения слоев изменилась на
du
, м;
–
градиент скорости, изменение скорости по нормали к направлению движения (с -1 ); m – коэффициент динамической вязкости (Па · с).
Если силу трения F
отнести к единице площади соприкасающихся слоев, то получим величину касательного напряжения t , и тогда (1.11) примет вид:
. (1.12)
Из (1.12) следует, что коэффициент динамической вязкости может быть определен как:
. (1.13)
Из (1.13) нетрудно установить физический смысл коэффициента динамической вязкости. При градиенте скорости =
1
; m
= t и выражает силу внутреннего трения, приходящуюся на единицу площади поверхности соприкасающихся слоев жидкости.
В практике, для характеристики вязкости жидкости, чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости n (м 2 /с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
. (1.14)
Вязкость жидкости зависит от рода жидкости, от температуры и от давления.
Зависимость вязкости минеральных масел, применяемых в гидросистемах, от давления p
при возрастании его до 50 МПа, можно определять с помощью приближенной эмпирической формулы:
, (1.15)
где n p
и
n
– кинематическая вязкость соответственно при давлении
p
и 0,1 МПа;
K
– опытный коэффициент, зависящий от марки масла: для легких масел (n 50 -6 м 2
/
с)
К =
0,02, для тяжелых масел (n
50
> 15 10 -6 м 2
/
с)
К =
0,03. При незначительных давлениях изменением вязкости пренебрегают. С повышением температуры вязкость жидкости уменьшается. Зависимость коэффициента кинематической вязкости от температуры определяется по эмпирической формуле:
.
(1.16)
Для смазочных масел, применяемых в машинах и гидросистемах, рекомендуется следующая зависимость:
, (1.17)
где n t – кинематическая вязкость при температуре t; n 50 –
кинематическая вязкость при температуре 50
0
С;
n
– показатель степени, зависящий от n 50, определяемый по формуле:
. (1.18)
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера ( 0 Е). Градус Энглера ( 0 Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости n применяется формула Убеллоде:
. (1.19)
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости в этом случае определяют по формуле:
, (1.20)
где с
– постоянная прибора;
Tж
– время истечения жидкости, с.
Дата добавления: 2015-12-08 ; ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
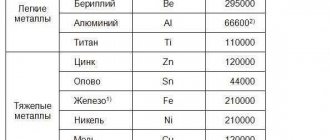
Некоторые значения
Приблизительные значения объёмного модуля упругости (К) для некоторых материалов
| Материал | Объёмный модуль упругости в ГПа | Объёмный модуль упругости в фунт-силе на квадратный дюйм |
| Стекло (см. также диаграмму ниже таблицы) | от 35 до 55 | 5,8×103 |
| Сталь | 160 | 23×103 |
| Алмаз[2] | 442 | 64×103 |
Приблизительный значения объёмного модуля упругости (K) для других веществ
| Вода | 2,2×109 Па (значение возрастает при более высоких давлениях) |
| Воздух | 1,42×105 Па (Адиабатический объёмный модуль упругости) |
| Воздух | 1,01×105 Па (объёмный модуль упругости при постоянной температуре) |
| Твёрдый гелий | 5×107 Па (приблизительно) |
Физические свойства жидкостей
Глава 1. ОСНОВЫ ГИДРОСТАТИКИ
Основными физическими свойствами жидкости являются: текучесть, плотность, удельный вес, вязкость, сжимаемость, температурное расширение.
Плотность жидкости – физическая величина, численно равная отношению массы жидкости к ее объёму.
(1.1)
где r
– плотность жидкости,
кг
/
м
3 ;
m
– масса жидкости;
кг
;
W
– объём жидкости,
м
3 .
Удельный вес – физическая величина, численно равная отношению веса жидкости к ее объёму.
(1.2)
где g
– удельный вес жидкости,
Н
/
м
3 ;
Между удельным весом g
и плотностью
r
имеется зависимость
(1.3
где g
= 9,81
м
/
с
2 – ускорение свободного падения.
Значения r
и
g
для воды и некоторых других жидкостей при различной температуре приведены в приложении 1.
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу смежных слоёв. Вязкость характеризуется коэффициентами динамической вязкости m
,
Па×с
, и
кинематической вязкости n
,
м
/
с
. Между этими коэффициентами имеется зависимость
(1.4)
Значения коэффициентов динамической и кинематической вязкости для некоторых жидкостей приведены в приложении 2.
Сжимаемость – свойство жидкости изменять свой объём при изменении давления. Сжимаемость характеризуется коэффициентом объёмного сжатия b
w, который можно определить по формуле
(1.5)
где b
w – коэффициент объёмного сжатия, 1/
Па
;
W
– первоначальный объём жидкости,
м
3 ;
DW
– изменение объёма жидкости,
м
3 ;
Dp
– изменение давления,
Па
.
Величина, обратная коэффициенту объёмного сжатия, называется модулем объёмной упругости К
. Модуль объёмной упругости измеряется в
Па
.
(1.6)
Коэффициенты объёмного сжатия жидкостей мало меняются при изменении температуры и давления. Значение коэффициентов объёмного сжатия и модулей упругости для некоторых жидкостей приведены в приложении 3.
Температурное расширение – свойство жидкости изменять свой объём при изменении температуры. Температурное расширение характеризуется коэффициентом температурного расширения , который может быть определен из выражения
(1.7)
где – коэффициент температурного расширения, 1/К
;
W
– первоначальный объём жидкости,
м
3 ;
– изменение объёма жидкости, м
3 ;
– изменение температуры, К
.
Коэффициенты температурного расширения для некоторых жидкостей приведены в приложении 4.
Задачи
1.1. Определить массу воды в рукаве диаметром 51 мм
и длиной 20
м.
Решение. Масса воды определяется из формулы (1.1)
Плотность воды по приложению 1
1.2. Определить вес воды в рукавах диаметром 66 мм
и 77
мм
и дли-ной 20
м
.
1.3. Определить массу дизельного мазута, находящегося в цистерне объёмом 50 м
3 , если плотность мазута составляет 920
кг
/
м
3 .
1.4. Определить, какой объём займет нефть, имеющая массу 20×10 3 кг
и плотность 900
кг
/
м
3 .
1.5. Определить плотность нефтепродуктов, если их масса составляет 17,5×10 3 кг
, объём 20
м
3 .
1.6. Определить вес этилового спирта в объёме 20 литров.
1.7. Уровень мазута в вертикальном цилиндрическом баке диаметром 2 м
понизился на 0,5
м
. Определить массу израсходованного мазута, если его плотность при температуре 20 °
С
равна 990
кг
/
м
3 .
1.8. При гидравлических испытаниях допускается утечка воды, которая за одни сутки не должна превышать 3 л
с квадратного метра смоченной поверхности. Возможно ли принять в эксплуатацию резервуар прямоугольной формы, имеющий размеры в плане 12´6
м
, в котором уровень воды за одни сутки понизился с 3,5
м
до 3,48
м
. Определить массу убывшей воды.
Решение. Объём убывшей воды составил
Масса убывшей воды
Площадь смоченной поверхности
Утечка воды с одного квадратного метра смоченной поверхности при гидравлических испытаниях
что превышает установленную норму.
1.9. Определить, возможно ли принять в эксплуатацию цилиндрический резервуар диаметром 12 м
, в котором уровень воды за одни сутки понизился с 5
м
до 4,985
м
.
1.10. Определить предельную массу воды, убывшей за одни сутки в результате гидравлических испытаний цилиндрического резервуара диаметром 18 м
. Определить предельное снижение уровня воды, если первоначальный уровень составлял 3,9
м
.
1.11. Определить коэффициент динамической вязкости нефти, если коэффициент кинематической вязкости составляет 0,624×10 -4 м
2 /
с
. Плотность нефти 750
кг
/
м
3 .
1.12. Водовод пожарного водопровода диаметром 300 мм
и длиной 50
м
, подготовленный к гидравлическим испытаниям, заполнен водой при атмосферном давлении. Определить объём воды, которую необходимо дополнительно подать в водовод, чтобы избыточное давление в нем поднялось до 5
МПа
. Деформацией труб водовода пренебречь.
Решение. Из уравнения (1.5) находим, что объём воды, который необходимо дополнительно подать в водовод, определяется как
Коэффициент объёмного сжатия воды
Первоначальный объём воды
1.13. При гидравлическом испытании технологического трубопровода длиной 200 м
и диаметром 250
мм
, заполненного керосином, давление было поднято до 1,5
МПа
. Через один час давление упало до 1,0
МПа
. Определить объём вытекшего через неплотность керосина. Коэффициент объёмного сжатия керосина принять = 80×10 -11 1/
Па
. Деформацией трубопровода пре- небречь.
1.14. Манометр на технологической емкости, полностью заполненной нефтью, показывает 0,5 МПа
. При выпуске 40
л
нефти показания манометра упали до 0,1
МПа
. Определить объём ёмкости, если коэффициент объёмного сжатия нефти = 80×10 -11 1/Па.
1.15. В вертикальном цилиндрическом резервуаре диаметром 5 м
находится 1,2×10 5
кг
нефти, плотность которой при 0 °
С
составляет 800
кг
/
м
3 . Определить колебания уровня нефти в резервуаре при изменении температуры от 0 °
С
до 30 °
С
.
1.16. Определить колебания уровня воды в баке водонапорной башни при изменении температуры от 10 °С
до 35 °
С
. В водонапорном баке диаметром 3
м
находится 20
м
3 воды. Коэффициент температурного расширения воды принять равным 2×10 -4 1/
К
.
1.17. Предельная высота уровня бензола в вертикальном цилиндрическом резервуаре диаметром 12 м
равна 10
м
при температуре 10 °
С
. Определить, до какого уровня возможно налить бензол при возможном повышении температуры до 30 °
С
. Расширением резервуара пренебречь.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения:
Да какие ж вы математики, если запаролиться нормально не можете.
8406 – | 7319 – или читать все.
193.151.241.65 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock! и обновите страницу (F5)
очень нужно
Примечания
- [hyperphysics.phy-astr.gsu.edu/hbase/permot3.html Bulk Elastic Properties]. hyperphysics
. Georgia State University. [www.webcitation.org/6AIhR7XkB Архивировано из первоисточника 30 августа 2012]. - (1985) «Calculation of bulk moduli of diamond and zinc-blende solids». Phys. Rev. B32
: 7988–7991. DOI:10.1103/PhysRevB.32.7988. Bibcode: [adsabs.harvard.edu/abs/1985PhRvB..32.7988C 1985PhRvB..32.7988C]. - Fluegel, Alexander
[www.glassproperties.com/bulk_modulus/ Bulk modulus calculation of glasses].
glassproperties.com
. [www.webcitation.org/6AIhRZh2a Архивировано из первоисточника 30 августа 2012].
| п • о • р Модули упругости для гомогенных изотропных материалов |
| Объёмный модуль упругости (K) | Модуль Юнга (E) | Параметры Ламе (\lambda) | Модуль сдвига (G) | Коэффициент Пуассона (\nu) | en:P-wave modulus (M) |
Отрывок, характеризующий Объёмный модуль упругости
– Ежели кто ко мне еще будет соваться, – сказал он, редко пропуская слова сквозь стиснутые и тонкие губы, – я того сейчас спущу вот сюда. Ну!… Сказав «ну»!, он повернулся опять, отпустил руки, взял бутылку и поднес ко рту, закинул назад голову и вскинул кверху свободную руку для перевеса. Один из лакеев, начавший подбирать стекла, остановился в согнутом положении, не спуская глаз с окна и спины Долохова. Анатоль стоял прямо, разинув глаза. Англичанин, выпятив вперед губы, смотрел сбоку. Тот, который останавливал, убежал в угол комнаты и лег на диван лицом к стене. Пьер закрыл лицо, и слабая улыбка, забывшись, осталась на его лице, хоть оно теперь выражало ужас и страх. Все молчали. Пьер отнял от глаз руки: Долохов сидел всё в том же положении, только голова загнулась назад, так что курчавые волосы затылка прикасались к воротнику рубахи, и рука с бутылкой поднималась всё выше и выше, содрогаясь и делая усилие. Бутылка видимо опорожнялась и с тем вместе поднималась, загибая голову. «Что же это так долго?» подумал Пьер. Ему казалось, что прошло больше получаса. Вдруг Долохов сделал движение назад спиной, и рука его нервически задрожала; этого содрогания было достаточно, чтобы сдвинуть всё тело, сидевшее на покатом откосе. Он сдвинулся весь, и еще сильнее задрожали, делая усилие, рука и голова его. Одна рука поднялась, чтобы схватиться за подоконник, но опять опустилась. Пьер опять закрыл глаза и сказал себе, что никогда уж не откроет их. Вдруг он почувствовал, что всё вокруг зашевелилось. Он взглянул: Долохов стоял на подоконнике, лицо его было бледно и весело. – Пуста! Он кинул бутылку англичанину, который ловко поймал ее. Долохов спрыгнул с окна. От него сильно пахло ромом. – Отлично! Молодцом! Вот так пари! Чорт вас возьми совсем! – кричали с разных сторон. Англичанин, достав кошелек, отсчитывал деньги. Долохов хмурился и молчал. Пьер вскочил на окно. Господа! Кто хочет со мною пари? Я то же сделаю, – вдруг крикнул он. – И пари не нужно, вот что. Вели дать бутылку. Я сделаю… вели дать. – Пускай, пускай! – сказал Долохов, улыбаясь. – Что ты? с ума сошел? Кто тебя пустит? У тебя и на лестнице голова кружится, – заговорили с разных сторон. – Я выпью, давай бутылку рому! – закричал Пьер, решительным и пьяным жестом ударяя по столу, и полез в окно. Его схватили за руки; но он был так силен, что далеко оттолкнул того, кто приблизился к нему. – Нет, его так не уломаешь ни за что, – говорил Анатоль, – постойте, я его обману. Послушай, я с тобой держу пари, но завтра, а теперь мы все едем к***. – Едем, – закричал Пьер, – едем!… И Мишку с собой берем… И он ухватил медведя, и, обняв и подняв его, стал кружиться с ним по комнате. Князь Василий исполнил обещание, данное на вечере у Анны Павловны княгине Друбецкой, просившей его о своем единственном сыне Борисе. О нем было доложено государю, и, не в пример другим, он был переведен в гвардию Семеновского полка прапорщиком. Но адъютантом или состоящим при Кутузове Борис так и не был назначен, несмотря на все хлопоты и происки Анны Михайловны. Вскоре после вечера Анны Павловны Анна Михайловна вернулась в Москву, прямо к своим богатым родственникам Ростовым, у которых она стояла в Москве и у которых с детства воспитывался и годами живал ее обожаемый Боренька, только что произведенный в армейские и тотчас же переведенный в гвардейские прапорщики. Гвардия уже вышла из Петербурга 10 го августа, и сын, оставшийся для обмундирования в Москве, должен был догнать ее по дороге в Радзивилов. У Ростовых были именинницы Натальи, мать и меньшая дочь. С утра, не переставая, подъезжали и отъезжали цуги, подвозившие поздравителей к большому, всей Москве известному дому графини Ростовой на Поварской. Графиня с красивой старшею дочерью и гостями, не перестававшими сменять один другого, сидели в гостиной.