Young's modulus of elasticity and shear, Poisson's ratio values (Table)
Elastic properties of bodies
Below are reference tables for commonly used constants; if two of them are known, then this is quite sufficient to determine the elastic properties of a homogeneous isotropic solid.
Young's modulus or modulus of longitudinal elasticity in dyn/cm2.
Shear modulus or torsional modulus G in dyn/cm2.
Compressive modulus or bulk modulus K in dynes/cm2.
Compressibility volume k=1/K/.
Poisson's ratio µ is equal to the ratio of transverse relative compression to longitudinal relative tension.
For a homogeneous isotropic solid material, the following relationships between these constants hold:
G = E / 2(1 + μ) - (α)
μ = (E / 2G) - 1 - (b)
K = E / 3(1 - 2μ) - (c)
Poisson's ratio has a positive sign and its value is usually between 0.25 and 0.5, but in some cases it can go beyond these limits. The degree of agreement between the observed values of µ and those calculated using formula (b) is an indicator of the isotropy of the material.
Tables of Young's Modulus of Elasticity, Shear Modulus and Poisson's Ratio
Values calculated from relations (a), (b), (c) are given in italics.
| Material at 18°C | Young's modulus E, 1011 dynes/cm2. | Shear modulus G, 1011 dynes/cm2. | Poisson's ratio µ | Modulus of bulk elasticity K, 1011 dynes/cm2. |
| Aluminum | 7,05 | 2,62 | 0,345 | 7,58 |
| Bismuth | 3,19 | 1,20 | 0,330 | 3,13 |
| Iron | 21,2 | 8,2 | 0,29 | 16,9 |
| Gold | 7,8 | 2,7 | 0,44 | 21,7 |
| Cadmium | 4,99 | 1,92 | 0,300 | 4,16 |
| Copper | 12,98 | 4,833 | 0,343 | 13,76 |
| Nickel | 20,4 | 7,9 | 0,280 | 16,1 |
| Platinum | 16,8 | 6,1 | 0,377 | 22,8 |
| Lead | 1,62 | 0,562 | 0,441 | 4,6 |
| Silver | 8,27 | 3,03 | 0,367 | 10,4 |
| Titanium | 11,6 | 4,38 | 0,32 | 10,7 |
| Zinc | 9,0 | 3,6 | 0,25 | 6,0 |
| Steel (1% C) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (soft) | 21,0 | 8,12 | 0,291 | 16,78 |
| Constantan 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Manganin | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) For steel containing about 1% C, elastic constants are known to change during heat treatment. 2) 60% Cu, 40% Ni. | ||||
The experimental results given below are for common laboratory materials, mainly wires.
| Substance | Young's modulus E, 1011 dynes/cm2. | Shear modulus G, 1011 dynes/cm2. | Poisson's ratio µ | Modulus of bulk elasticity K, 1011 dynes/cm2. |
| Bronze (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Copper | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Nickel silver1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Glass | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Glass yen crowns | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Jena flint glass | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Welding iron | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Cast iron | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Magnesium | 4,25 | 1,63 | 0,30 | — |
| Phosphor bronze2) | 12,0 | 4,36 | 0,38 | — |
| Platinoid3) | 13,6 | 3,6 | 0,37 | — |
| Quartz threads (floating) | 7,3 | 3,1 | 0,17 | 3,7 |
| Soft vulcanized rubber | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Steel | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Zinc | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92.5% Cu, 7% Sn, 0.5% P 3) Nickel silver with a small amount of tungsten. | ||||
| Substance | Young's modulus E, 1011 dynes/cm2. | Substance | Young's modulus E, 1011 dynes/cm2. |
| Zinc (pure) | 9,0 | Oak | 1,3 |
| Iridium | 52,0 | Pine | 0,9 |
| Rhodium | 29,0 | Red tree | 0,88 |
| Tantalum | 18,6 | Zirconium | 7,4 |
| Invar | 17,6 | Titanium | 10,5-11,0 |
| Alloy 90% Pt, 10% Ir | 21,0 | Calcium | 2,0-2,5 |
| Duralumin | 7,1 | Lead | 0,7-1,6 |
| Silk threads1 | 0,65 | Teak | 1,66 |
| Web2 | 0,3 | Silver | 7,1-8,3 |
| Catgut | 0,32 | Plastics: | |
| Ice (-20C) | 0,28 | Thermoplastic | 0,14-0,28 |
| Quartz | 7,3 | Thermoset | 0,35-1,1 |
| Marble | 3,0-4,0 | Tungsten | 41,1 |
| 1) Rapidly decreases with increasing load 2) Detects noticeable elastic fatigue | |||
| Temperature coefficient (at 150C) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Compressibility k, bar-1 (at 7-110C) | |||
| ɑ, for E | ɑ, for G | |||
| Aluminum | 4,8*10-4 | 5,2*10-4 | Aluminum | 1,36*10-6 |
| Brass | 3,7*10-4 | 4,6*10-4 | Copper | 0,73*10-6 |
| Gold | 4,8*10-4 | 3,3*10-4 | Gold | 0,61*10-6 |
| Iron | 2,3*10-4 | 2,8*10-4 | Lead | 2,1*10-6 |
| Steel | 2,4*10-4 | 2,6*10-4 | Magnesium | 2,8*10-6 |
| Platinum | 0,98*10-4 | 1,0*10-4 | Platinum | 0,36*10-6 |
| Silver | 7,5*10-4 | 4,5*10-4 | Flint glass | 3,0*10-6 |
| Tin | — | 5,9*10-4 | German glass | 2,57*10-6 |
| Copper | 3,0*10-4 | 3,1*10-4 | Steel | 0,59*10-6 |
| Nickel silver | — | 6,5*10-4 | ||
| Phosphor bronze | — | 3,0*10-4 | ||
| Quartz threads | -1,5*10-4 | -1,1*10-4 | ||
Young's modulus (of elasticity)
All solids, both crystalline and amorphous, have the property of changing their shape under the influence of force applied to them. In other words, they are subject to deformation.
If a body returns to its original size and shape after the external force ceases its influence, then it is called elastic, and its deformation is considered elastic.
For any body, there is a limit to the applied force, after which the deformation ceases to be elastic, the body does not return to its original shape and original dimensions, but remains in a deformed state or collapses. The theory of elastic deformations of bodies was created at the end of the 17th century by the British scientist R.
Hooke and developed in the works of his compatriot Thomas Young. Hooke's and Young's law and coefficient, which determine the degree of elasticity of bodies, were named in their honor, respectively. It is actively used in engineering during calculations of the strength of structures and products.
Young's modulus
Definition and overview of shear deformation
The main feature characterizing shear deformation is the preservation of constant volume. Regardless of the direction in which the force factors act, this parameter remains unchanged.
Examples of shear deformation can be found during various types of work. Such cases include:
- when sawing timber;
- cutting or chopping metal;
- as a result of violation of the integrity of the fastening of metal or wooden parts connected by hardware;
- beams in places where supports are attached;
- places where bridge spans are fastened;
- fasteners on the jumpers for connecting railway rails;
- cutting a sheet of paper with scissors.
Under certain conditions, a net shift occurs. It is defined as a shear in which all four faces (for example, a rectangular part) are affected only by stresses directed tangentially to the surface. In this case, there will be a smooth shift of all layers of the part from the upper to the lower layers. Then the external force changes the shape of the part, but the volume remains unchanged.
To assess the magnitude of the shift and the reliability of the structure, the following parameters are used:
- magnitude, direction and point of application of the acting force;
- shear modulus;
- angle of change of the external edges of the product;
- tangential stress;
- torsion modulus (depends on the physical and mechanical characteristics of the material);
Calculation and practical measurement of these parameters are necessary to assess the stability and integrity of the structure. The formula that allows you to calculate permissible changes takes into account all the impacts on specific layers of the part and the entire structure as a whole.
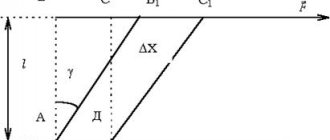
The main final parameters are absolute and relative shift. It is called absolute when the angle of the resulting deviation from the initial position of the face is equal. Relative is equal to the quotient of the deviation value divided by the distance between the faces located on opposite sides. During elastic shear deformation, some elements undergo compression and others undergo expansion.
In the case of deformation, the angle is considered proportional to the external force. Increasing the degree of impact can transform the shear deformation into shearing. This will lead to the destruction of not only the fastening elements (bolts, studs, rivets), but also the entire part.
For clarity, the change in the shape of a part during shear deformation is indicated by the dynamics of the process using the magnitude of the displacement angle and the vectors of the resulting stresses. The acting force is directed towards the displacement of the layers of the part under consideration.
In modern conditions, the shear angle is measured by various technical instruments. The main device for measuring displacement parameters is a strain gauge. These devices operate on different physical principles:
- optical (including laser);
- acoustic;
- X-ray; electrical;
- pneumatic.
In these devices, the relative shear deformation is processed using modern computing facilities using appropriate software. Each method has its own advantages and disadvantages. Their use depends on the task at hand, technical and financial feasibility.
Shear modulus of metals
The shear modulus of metals, as a rule, decreases with increasing temperature. At high pressures, the shear modulus also appears to increase with increasing applied pressure. Correlations between melting point, vacancy formation energy, and shear modulus have been observed in many metals.
Several models exist that attempt to predict the shear modulus of metals (and possibly alloys). Shear modulus models that have been used in plastic flow calculations include:
- The MTS shear modulus model is developed and used in combination with the mechanical Threshold Force plastic flow stress (MSF) model.
- The Steinberg-Cochran-Guinan (SCG) shear modulus model is developed and used in conjunction with the Steinberg-Cochran-Guinan-Lund (SCGL) flow stress model.
- Nadal and LePoac (NP), a shear modulus model that uses Lindemann's theory to determine the temperature dependence and the SCG model for the pressure–shear modulus dependence.
MTS shear modulus model
The MTS shear modulus model has the form:
μ ( T ) = μ 0 — D exp ( T 0 / T ) — 1 — / T) -1>>>
where is the shear modulus at , and and are the material constants. μ 0 > T = 0 K DT 0 >
SKG shear modulus model
Steinberg-Cochran-Guinan (SCG) Model of the shear modulus depends on pressure and has the form
μ ( n , T ) = μ 0 + ∂ μ ∂ n n η 1 / 3 + ∂ μ ∂ T ( T — 300 ) ; η = ρ / ρ 0 + > >> + > (T-300); Quad ETA: =Rho/Rho_>
where μ is the shear modulus in the reference state ( T
= 300 K,
p
= 0, η = 1),
p
represents pressure and
T
represents temperature.
Model NP shear modulus
The Nadal-Le Poac (NP) shear modulus model is a modified version of the SCG model. The empirical temperature dependence of the shear modulus in the SCG model is replaced by an equation based on Lindemann's melting theory. The NP shear modulus model has the form:
T right]; quad-core C: = ) ^ > > >
J ( T ^ ) = 1 + exp [ — 1 + 1 / ζ 1 + ζ / ( 1 — T ^ ) ] for T ^ = TT m ∈ [ 0 , 1 + ζ ] , > (>): = 1+ exp left [->)>> right] quad > quad >: = >> in [0, 1+ zeta]>
and μ is the shear modulus at 0 K and ambient pressure, ζ is the material parameter, k b
is Boltzmann's constant,
m
is the atomic mass, and
e
is Lindemann's constant.
Basic information
Young's modulus (also called the longitudinal modulus of elasticity and the modulus of elasticity of the first kind) is an important mechanical characteristic of a substance. It is a measure of resistance to longitudinal deformation and determines the degree of rigidity. It is designated as E; measured in n/m 2 or in Pa.
This important coefficient is used when calculating the rigidity of workpieces, assemblies and structures, and in determining their resistance to longitudinal deformations. Substances used for the manufacture of industrial and building structures, as a rule, have very large E values. And therefore, in practice, E values for them are given in gigaPascals (10 12 Pa)
The value of E for rods can be calculated; for more complex structures it is measured during experiments.
Approximate values of E can be obtained from the graph constructed during tensile tests.
Tensile test schedule
E is the quotient of normal stress σ divided by relative elongation ε.
Hooke's law can also be formulated using Young's modulus.
Shear stress
The influence of an external force on the edge leads to a change in shape in the product. All stresses are divided into two categories: normal and tangential. Internal stresses that arise in various layers of a product subject to deformation are considered normal.
Shear stresses and strains are described using analytical expressions and graphical representations. The general state is described by spatial (three-coordinate) stress. If in a particular case it is possible to identify sections in which both types of stresses are equal to zero, we can move on to simpler models for describing this process. They are a two-coordinate (flat) stress state or a linear one. The last two models are special cases of a three-coordinate stress state.
Shear stress is a measure of the slip of one transverse layer relative to another. In changes on the surface of each layer, only shear stresses occur. To assess the complete picture of deformation, the following theoretical principles are used:
- law of pairing of tangential stresses;
- calculation of extreme normal stresses;
- determination of all tangential stresses.
Evaluating them all under displacement deformation will allow the strength of the structure to be assessed.
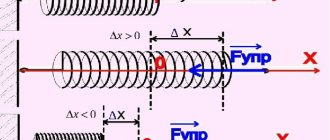
Shear modulus
In materials science, shear modulus
or
stiffness modulus
, denoted
G
, or sometimes
S
or
μ
, is defined as the ratio of shear stress to shear strain:
g = d e e τ x Y γ x Y = F / A Δ x / L = FLA Δ x > > > >> = > = >>
τ X Y = F / A = F / A > = Shear stress F is the force that acts A is the area on which the force acts γ X Y > = Shear strain. In engineering, elsewhere = Δ x / L = tan θ = θ Δ x is the lateral displacement L initial length
The resulting SI unit of shear modulus is the pascal (Pa), although it is usually expressed in gigapascals (GP) or thousand pounds per square inch (kg per square inch). Its dimensional form is M 1 l -1 T -2, replacing the forces
by
mass
times
acceleration
.
Modulus of elasticity - what is it?
The elastic modulus of any material is a set of physical quantities
, which characterize the ability of a solid body to elastically deform under conditions of force applied to it. It is expressed by the letter E. So it will be mentioned in all the tables that will go further in the article.
It is impossible to say that there is only one way to determine the value of elasticity. Different approaches to the study of this quantity have led to the fact that there are several different approaches at once. Below are three main ways to calculate the indicators of this characteristic for different materials: