Definition and formula of body weight
Definition
In Newtonian mechanics, the mass of a body is a scalar physical quantity, which is a measure of its inertial properties and a source of gravitational interaction. In classical physics, mass is always a positive quantity.
Weight
– an additive quantity, which means: the mass of each set of material points (m) is equal to the sum of the masses of all individual parts of the system (mi):
$$m=\sum_{i=1}^{n} m_{i}(1)$$
In classical mechanics they consider:
- body weight is not dependent on the movement of the body, the influence of other bodies, or the location of the body;
- the law of conservation of mass is satisfied: the mass of a closed mechanical system of bodies is constant over time.
Formulas for inertia
In physics, the formula for finding inertial mass is as follows:
m = F/a
Here F is the force that acts on the body and causes it to experience acceleration a. The formula shows that the greater the acting force and the less it imparts acceleration to the body, the greater the inertial mass m.
In addition to the written expression, one more formula for finding mass in physics should be given, which is related to the phenomenon of inertia. This formula looks like:
m = p/v
Here p is the amount of motion (impulse), v is the speed of the body. The more motion a body has and the lower its speed, the greater the inertial mass it has.
Gravitational mass
The mass of a material point is included in the law of universal gravitation, and it determines the gravitational properties of a given point. At the same time, it is called gravitational (heavy) mass.
It has been empirically found that for all bodies the ratio of inertial masses to gravitational ones is the same. Consequently, if we correctly choose the value of the constant gravity, we can obtain that for any body the inertial and gravitational masses are the same and are associated with the force of gravity (Ft) of the selected body:
$$m=\frac{F_{t}}{g}(3)$$
where g is the acceleration of free fall. If observations are made at the same point, then the accelerations of gravity are the same.
Relative
The concept of relative mass is used in atomic physics and chemistry. Since the masses of atoms and molecules have very small values (≈10-27 kg), it turns out to be extremely inconvenient to operate with them in practice when solving problems. Therefore, the community of scientists decided to use the so-called relative mass, that is, the quantity in question is expressed in units of mass relative to the mass of a known standard. This standard was 1/12 of the mass of a carbon atom, which is equal to 1.66057 * 10-27 kg. The corresponding relative value is called the atomic unit (a.u.m.).
The relative mass formula M can be written as follows:
M = ma / (1 / 12 * mC)
Where ma is the mass of the atom in kilograms, mC is the mass of the carbon atom in kilograms. For example, if we substitute the value of the mass of an oxygen atom into this expression, then its a. e.m. will be equal to:
M = 26.5606 * 10-27 / (1.66057 * 10-27) = 15.9949.
Since a. e.m. is a relative quantity, then it has no dimension.
The convenience of using this term in practice lies not only in the small and whole values of this unit of measurement. The point is that the value of a. e.m. is the same in size as the molar mass expressed in grams. The latter is the mass of one mole of a substance.
Mass in special relativity
In SRT, mass is invariant, but not additive. It is defined here as:
$$m=\sqrt{\frac{E^{2}}{c^{4}}-\frac{p^{2}}{c^{2}}}$$
where E is the total energy of a free body, p is the momentum of the body, c is the speed of light.
The relativistic mass of a particle is determined by the formula:
$$m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}(7)$$
where m0 is the rest mass of the particle, v is the speed of the particle.
The basic unit of mass in the SI system is: [m]=kg.
In GHS: [m]=gr.
Entertaining tasks
After clarifying the question of what mass is, you can begin to solve problems. Those that have entertaining content will interest students more.
Task No. 1. Condition: Winnie the Pooh was given two identical liter pots. One of them contains honey, the other contains oil. How to find out which honey is in it without opening them?
Solution. The density of honey is greater than that of butter. The first has a value of 1430 kg/m3, and the second - 920 kg/m3. Therefore, with the same volume of pots, the one with honey will be heavier.
To more accurately answer the question of the problem, you will need to calculate the mass of honey and butter in the pots. Their volume is known - it is 1 liter. But the calculations will require a value in cubic meters. Therefore, you need to do the translation first. One m3 contains 1000 liters. Therefore, when calculating the result, you will need to take a volume value equal to 0.001 m3.
Now the mass formula can be used, where density is multiplied by volume. After simple calculations, the following mass values are obtained: 1.43 kg and 0.92 kg, for honey and butter, respectively.
Answer: The honey pot is heavier.
Problem No. 2. Condition: The clown easily lifts a weight on which it is written that its mass is 500 kilograms. What is the actual mass of a weight if its volume is 5 liters and the substance from which it is made is cork?
Solution. In the table you need to find the density value of the plug. It is equal to 240 kg/m3. Now you need to convert the volume value, you get 0.005 m3.
Knowing these values, it is not difficult to use the already known formula to calculate the mass of a fake weight. It turns out to be 1.2 kg. Now it’s clear why it’s not hard for the clown at all.
Answer. The actual mass of the weight is 1.2 kg.
Problem No. 3. Condition: The genie was sitting in a lamp whose volume is unknown. But its density at that moment was 40,000 kg/m3. When it was released from the bottle, it began to have the parameters of an ordinary human body: volume 0.08 m3, density 1000 kg/m3. What is the volume of the lamp?
Solution. First you need to find out its mass in normal condition. It will be equal to 80 kg. Now you can move on to finding the volume of the lamp. Let's assume that Jin occupies all the space inside it. Then you will need to divide the mass by the density, that is, 80 by 40000. The result will be a value of 0.002 m3. Which is equal to two liters.
Answer. The volume of the lamp is 2 liters.
Body weight
Weight is the force exerted by the body on a support or suspension. Weight is measured, like any other force, in Newtons.
“But wait! Weight is measured in kilograms - I weigh 50.”
This is not entirely true. In everyday life, we often replace the concept of “mass” with the concept of “weight” and say: the weight of a suitcase is ten kilograms. In physics, these are two completely different concepts, which are interconnected.
If you have a scale nearby, we invite you to experiment! One caveat: our idea will work with mechanical scales, but not with electronic ones. Go!
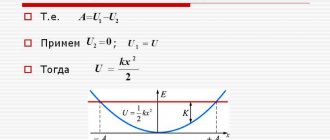
Step 1. If you stand on the scales straight and do not move, your weight will be calculated according to the formula:
| P = mg P - body weight [N] m—mass [kg] g—gravitational acceleration [m/s2] On planet Earth g = 9.8 m/s2 |
Two objections may arise here:
- It's gravity, not weight. The formula is the same!
- On the scales the mass is displayed in kilograms. And if I multiply my mass by the acceleration of gravity, I will clearly get a number almost 10 times greater than what the scales show.
Point of application of force. This formula is indeed similar to gravity. The weight of a body at rest is numerically equal to the mass of the body; the difference is only in the point of application of force.
Gravity is the force with which the Earth acts on the body, and weight is the force with which the body acts on the support. This means that they will have different points of application: gravity to the center of mass of the body, and weight to the support.
Scales measure strength. Scales work in such a way that they measure the weight of the body - the force with which we act on them, and show - mass. We can conclude that the scale is a dynamometer (a device that measures force).
Let's continue the experiment.
Step 2. Now let's play around and stand up on our tiptoes! The arrow deviated sharply to the left, and then returned to its place. You have given yourself an upward acceleration, while the free fall acceleration is always directed toward the center of the Earth (downward).
Now we calculate body weight using the formula:
| P = m(ga) P - body weight [N] m—mass [kg] g—gravitational acceleration [m/s2] a is your acceleration [m/s2] On planet Earth g = 9.8 m/s2 |
Step 3. The last part of the experiment is to drop sharply onto your heels. Now you're pushing harder on the scale because you've added downward acceleration. The scale arrow will deviate to the right and return to its place when you come to a state of rest.
The weight formula will take the form:
| P = m(g+a) P - body weight [N] m—mass [kg] g—gravitational acceleration [m/s2] a is your acceleration [m/s2] On planet Earth g = 9.8 m/s2 |
By the way, if you stand straight on the scales, but weigh yourself in the elevator, everything will work the other way around. If the elevator goes up, then it seems to press the scales on the person standing on them, and this is exactly the situation with increasing weight. And if it’s down, the scales seem to “run away” from you to show a lower value.
We can describe this case through Newton's 2nd law . Let's take an elevator that goes down. Let us denote the forces in the figure.
N – ground reaction force [N];
mg – gravity [N];
a is the acceleration with which the elevator moves [m/s2].
N + mg = ma
When projecting onto the downward y-axis, we get:
-N + mg = ma
And now we need Newton’s third law - according to it, the support reaction force is equal to the weight of the body:
P=N
-P + mg = ma
P = m(ga)
How to convert volume to mass in physics?
Having become familiar with the definition of all the necessary quantities, we will move directly to the answer to the question of the article. To convert volume to mass, we use the definition of matter density: ρ = m/V. From this formula we express the mass, we get: m = ρ*V.
Thus, if the volume of a body and the density of the substance of which this body consists are known, then it is enough to multiply these values to obtain the mass of the body, which is the answer to the question of how to convert volume into mass. It should be remembered that before multiplying volume and density, it is necessary to convert them to the appropriate units of measurement, for example to [m3] and [kg/m3], respectively.
On the contrary, to convert mass into volume, the following formula is suitable: V = m/ρ, that is, the mass of the body must be divided by its density.
Training tasks
1. An excess of sodium sulfate solution was added to 300 g of barium nitrate solution. The mass of the precipitate formed was 23.3 g. Determine the concentration of salt in the original solution.
2. An excess of barium chloride solution was added to 150 g of sodium sulfate solution. The mass of the precipitate formed was 23.3 g. Determine the concentration of salt in the original solution.
3. An excess of calcium nitrate solution was added to 300 g of sodium silicate solution. The mass of the precipitate formed was 12.0 g. Determine the salt concentration in the original solution.
4. An excess of hydrochloric acid solution was added to 150 g of potassium carbonate solution. At the same time, gas with a volume of 3.36 liters (no.) was released. Determine the salt concentration in the original solution.
5. An excess of hydrobromic acid solution was added to 250 g of sodium bicarbonate solution. At the same time, gas with a volume of 5.6 liters was released. Determine the salt concentration in the original solution.
6. An excess of barium chloride solution was added to 50 g of sodium carbonate solution. The mass of the precipitate formed was 7.88 g. Determine the concentration of salt in the original solution.
7. An excess of potassium carbonate solution was added to 200 g of barium chloride solution. The mass of the precipitate formed was 7.88 g. Determine the concentration of salt in the original solution.
8. An excess potassium hydroxide solution was added to 200 g of iron (II) chloride solution. The mass of the precipitate formed was 18.0 g. Determine the concentration of salt in the original solution.
9. An excess of sodium iodide solution was added to 400 g of lead nitrate solution. The mass of the precipitate formed was 23.05 g. Determine the concentration of salt in the original solution.
10. An excess of lead nitrate solution was added to 300 g of sodium iodide solution. The mass of the precipitate formed was 23.05 g. Determine the concentration of salt in the original solution.
11. Determine the mass of the precipitate that will form when 150 g of a 14.8% calcium chloride solution reacts with an excess sodium carbonate solution.
12. Determine the volume of gas (n.o.) that will be released when 120 g of 8.8% sodium carbonate solution reacts with an excess of hydrochloric acid solution.
13. Determine the mass of salt that will precipitate when 140 g of a 13.5% solution of zinc nitrate reacts with an excess solution of sodium sulfide.
14. Determine the mass of the precipitate that will be released when 200 g of an 18.8% copper nitrate solution reacts with an excess sodium sulfide solution.
15. Determine the mass of the precipitate that will form when 200 g of a 6.1% sodium silicate solution reacts with an excess zinc chloride solution.
16. Determine the mass of the precipitate that will be released when 200 g of a 12.7% solution of iron (II) chloride reacts with an excess of sodium sulfide solution.
17. Determine the mass of the precipitate that will be released when 50 g of a 17% solution of silver nitrate reacts with an excess solution of potassium bromide.
18. Determine the mass of the precipitate that is formed when 200 g of a 6.1% sodium silicate solution reacts with an excess calcium nitrate solution.
19. Determine the mass of the precipitate that is formed when 50 g of a 5.8% solution of magnesium chloride reacts with an excess of sodium phosphate solution.
20. Determine the volume of gas that will be released when 200 g of a 6.9% solution of potassium carbonate reacts with an excess of hydrochloric acid solution.
21. Phosphorus (V) oxide weighing 21.3 g was dissolved in a solution of potassium hydroxide, resulting in a solution of average salt weighing 500 g. Determine the concentration of potassium phosphate in the final solution.
22. The iron(II) chloride solution reacted completely with 120 g of sodium hydroxide solution, resulting in the formation of 6.0 g of precipitate. Determine the mass fraction of sodium hydroxide in the original solution.
23. What volume of ammonia (n.a.) can completely react with 150 g of a 20% solution of sulfuric acid to form an average salt?
24. Magnesium was dissolved in 200 g of a 20% hydrochloric acid solution until gas evolution stopped. Determine the volume of hydrogen released during this process (n.u.).
25. Ammonia with a volume of 10 liters (no.) was passed through a solution of sulfuric acid with a mass fraction of 8% until an average salt was formed. Determine the mass of the original solution.
26. Determine the volume of hydrogen sulfide (NS) that must be passed through 130 g of a 6% solution of copper (II) chloride until copper (II) sulfide is completely precipitated.
27. Hydrogen sulfide with a volume of 3.36 l (N.S.) was passed through a solution of sodium hydroxide, resulting in 180 g of sodium sulfide solution. Determine the mass fraction of salt in the resulting solution.
28. Aluminum weighing 8.1 g can completely react with 250 g of sulfuric acid solution. Determine the mass fraction of sulfuric acid in the original solution.
29. A solution of potassium chloride was added to 250 g of a solution of silver nitrate until the precipitation of a precipitate stopped, the mass of which was 14.35 g. Determine the mass fraction of silver nitrate in the original solution.
30. An excess of potassium phosphate solution was added to 300 g of a 5% magnesium chloride solution. Calculate the mass of the precipitate that fell.