Concept of spring potential energy
When considering what the potential energy of a spring is, attention should be paid to the concept itself - a property that bodies can have when they are on the ground. This point determines that a wide variety of products, including the one in question, can have it. The features of the concept under consideration include the following:
- Potential energy in the case under consideration is formed due to a change in state. Even with an insignificant displacement of the turns relative to each other, it is considered a change in the state of such a product.
- In order to change the state of the product, a certain action is performed. This often requires effort. In this case, it is important to calculate the required force to compress the coils.
- After doing a certain job, most of the effort that was spent on performing the action is released under certain circumstances. Typically, this process involves returning the coils to their original position. This is achieved through the special shape of the product, as well as the use of appropriate material that has increased elasticity. It is due to this property that the product in question is often installed. The indicator can reach very high levels, which is sufficient to implement various tasks. A common example is the installation of springs in locking and safety elements, which are responsible for directly returning the locking element to the required position.
It is also widely used in the creation of a wide variety of mechanisms, for example, winding watches. When designing various mechanisms, the law of conservation of mechanical force is taken into account, which is characterized by a fairly large number of features.
Calculation of the work of elastic force
The load has made a known displacement, we also know the magnitude of the elastic force, the vectors of displacement and elastic force are parallel. It would seem that everything is clear - you need to multiply the magnitude of the force by the magnitude of the displacement and get the value of the work. However, everything is not so simple here - let's figure out why.
What does the formula that expresses the magnitude of the elastic force tell us? The fact that the elastic force is not a constant quantity, it changes as the load moves. And indeed, the magnitude of this force, as we see from the formula, depends on the coordinates of the center of the load. The formula for the work of force, which we used earlier, is valid only if the force does not change its magnitude as it moves. How then? One way out of this situation could be that we apply the same method that we used earlier in the kinematics section when calculating the displacement of a body moving with uniform acceleration.
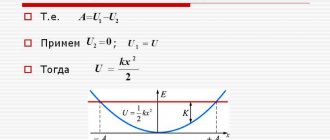
The entire trajectory of the load can be divided into very small sections (sections within which the elastic force can be considered almost constant). Further, within each such area, we can calculate the work of the elastic force due to its practical constancy. Then the work on the entire cargo movement area will be made up of all these small works in these areas. Thus, we can calculate the work of the elastic force along the entire trajectory of the load. In Fig. 4 shows the details of such a calculation.
Rice. 4. Dependence of the elastic force on the coordinate of motion
It can be seen that if we plot on the graph the dependence of the modulus of the elastic force on the modulus of the coordinates of the load, then do the above-described division into small sections, then the amount of work in each small section is numerically equal to the area of the figure limited by the graph: the x-axis and two perpendiculars to this axis (cm Fig. 5).
Rice. 5. Area of the figure
If we sum up the value of the work in each area (the area of small figures), we obtain the area of the large figure shown in Fig. 6.
Rice. 6. Area of a large figure
Since this figure is a rectangular trapezoid, we can use the formula to calculate the area of such a figure - this is half the sum of the bases multiplied by the height. As a result of the transformations, we obtain the following formula - the work is equal to the difference between the value:
This result can be reached in a slightly different way. To calculate the work of the elastic force in this method, you simply need to take the average value of the elastic force and multiply it by the displacement of the body. This statement can be written as:
,
where is the average value of the elastic force, which is equal to half the sum of its initial and final values. If we substitute this expression into the formula for work, then using simple algebraic transformations we get the same expression that we received earlier:
As can be seen from this formula, the work depends only on the initial and final coordinates of the center of the load, and one more note: as can be seen from the last formula, the work of the elastic force in no way depends on the mass of the load. This is due to the fact that the elastic force itself does not depend on this mass.
Now let's take a closer look at the last formula - if we take -1 out of brackets, we find that the work is the difference taken with a minus sign between the values of a certain quantity, equal to half the product of the spring stiffness and the square of its elongation at the final and initial moments of time.
Let's remember what we did when calculating the work of gravity in the last lesson. That time we encountered a new physical quantity for us, the difference between the values of which at the final and initial moments of time was equal to the work of gravity taken with the “-” sign. This value is equal to the product of the mass of the body by the acceleration of gravity and the height to which the body was raised above a certain level, we called the potential energy of the body raised above the ground.
Law of conservation of mechanical energy
According to established laws, the mechanical effect of a conservative mechanical system is maintained over time. This moment determines that the potential energy of a deformed spring cannot arise on its own or disappear somewhere. That is why you need to make an appropriate effort to create it.
The law under consideration belongs to the category of integral equalities. This pattern determines that it is the result of the action of differential laws and is a property or sign of the cumulative impact.
To carry out the corresponding calculations, a certain formula must be applied. The force with which the impact is exerted is not constant. That is why the graphical method is used to calculate it. The simplest relationship can be described as follows: F=kx. When applying such a dependence, the constructed coordinate line will be represented by a straight line, which is located at an angle relative to the coordinate system.
Potential energy can be attributed to such a device only if it is equal to the maximum work and does not depend on the conditional trajectory of movement. Conducted studies indicate that such work obeys Hooke's law. To determine the main indicator, the following formula is used: U=kk2/2.
To deform the turns, a certain force must be applied to them, since otherwise the kinetic force will not arise.
Understanding Hooke's Law
All natural objects can be deformed, i.e. change its shape or volume under the influence of applied force. If such deformations (i.e. changes) disappear after the applied force ceases, then they are called elastic. Elasticity plays an important role in technology. Elastic springs are used to absorb shock when a spacecraft lands on the surface of a planet. Elastic plates rolled into a spiral are used in watch winding mechanisms. Even a mousetrap uses the elastic deformation of a spring.
Back in the 17th century, the English physicist Robert Hooke, while studying the elastic properties of various materials, derived a law named after him. According to Hooke's law, elastic deformation of a material requires the application of a force whose magnitude is directly proportional to its deformation. For example, to stretch a spring by the amount \( x \), you will need to apply an external force \( F_{ext} \), which is equal to:
where \( k \) is the proportionality coefficient.
More precisely, the deformation vector \( \mathbf{x} \) is always directed opposite to the spring resistance force (or elastic force) \( \mathbf{F} \), and therefore the vector formulation of Hooke’s law usually includes a “minus” sign :
Stretching and compressing springs
It should be remembered that Hooke's law applies only to elastically deformable materials.
In the real world, in addition to elastic deformations, there are also plastic deformations. This is the name for deformations that remain in an object, at least partially, even after the cessation of external forces. If the force does not exceed a certain known value, which is called the elastic limit, then the resulting deformation will be plastic. The elastic limit has different values for different materials. If a deformable object, such as a spring, experiences only elastic deformations, then it is called ideally elastic, for example, a perfectly elastic spring. The proportionality coefficient \( k \) in Hooke's law \( F=kx \) is called the elasticity coefficient of the object, which depends on the material of the object, its dimensions and is measured in N/m.
Let's say you need to design a suspension for a car weighing 1000 kg, consisting of 4 springs that can perfectly elastically deform over a distance of 0.5 m. What elasticity coefficient must the spring have to support the weight of the car?
The weight of the car is equal to \( mg \), where \( g \) is the acceleration due to gravity under the influence of gravitational attraction. This means that each spring bears four times less load \( mg/4 \).
Let us determine the elastic deformation of the spring under the influence of this load using the formula of Hooke’s law:
those. the elasticity coefficient is:
Substituting the values, we get:
So, to support the weight of the car, you will need a spring with an elasticity coefficient equal to 4.9 103 N/m. Do not forget that each element of the car's suspension must have a certain margin of strength in order to withstand unpredictable excess loads, for example on potholes. However, this task is beyond the scope of this course.
We study the features of Hooke's law
As mentioned above, the vector formulation of Hooke’s law usually includes a minus sign:
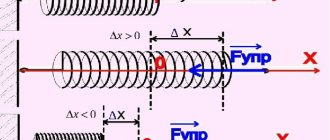
Thus, the minus sign expresses the following feature of elastic deformation: the elastic force is always opposite to the deformation. In Fig. 12.1 schematically shows the directions of the elastic force and deformation during compression and tension of the spring.
As you can see, in the absence of tension or compression, there is no deformation (see diagram A in Fig. 12.1). If the spring is compressed to the left, then the elastic force is directed to the right (see diagram B in Fig. 12.1), and if the spring is stretched to the right, then the elastic force is directed to the left (see diagram B in Fig. 12.1).
It is not for nothing that the elastic force of a spring is called the resistance force, because it strives to establish equilibrium.
Rigid body dynamics
Some expressions (determined by applying the most appropriate formulas) can only be determined by taking into account the rules regarding the dynamics of solid objects. An entire section is devoted to this issue. When calculating the potential energy of a compressed spring, some of the laws in this section also apply
The dynamics of a rigid body is considered because in most cases the mechanism performs an action associated with the direct movement of an object.
The considered property of the product can change depending on the dynamics of the solid body. This is due to the fact that the product is also influenced by the environment. An example is friction or heat.
Average kinetic energy
Kinetic energy is the energy determined by the speed of movement of different points that belong to this system. However, it should be remembered that it is necessary to distinguish between 2 energies that characterize different types of motion: translational and rotational. In this case, the average kinetic energy (AKE) is the average difference between the totality of the energies of the entire system and its rest energy, that is, in fact, its value is the average value of potential energy. The formula for average kinetic energy is:
where k is Boltzmann's constant; T is temperature. It is this equation that is the basis of molecular kinetic theory.
Moment of force and moment of impulse about the axis
The deformation of the spring is also considered taking into account the moment of force and momentum relative to the axis. These two parameters allow you to calculate all the required indicators with higher accuracy. A fairly common question is what the moment of force is - a vector quantity that is determined by the vector product of the radius and the vector of the applied force.
Momentum is a quantity that is used to determine the amount of rotational motion.
Among the features of this indicator are the following:
- Rotation mass. An object can have different masses.
- Distribution relative to the axis. The axis can be located at different distances from the object itself.
- Rotational speed. This property is considered the most important; depending on the design, it can be constant or change.
The calculation of each indicator is carried out by applying the appropriate formula. In some cases, the required input data is measured, without which calculations will not be possible.
Impulse of a system of bodies
The momentum of a system of bodies is equal to the vector sum of the momentum of the bodies that make up this system:
When considering any mechanical problem, we are interested in the motion of a certain number of bodies. The set of bodies whose movement we study is called a mechanical system or simply a system.
Let us consider a system consisting of three bodies. External forces act on the bodies of the system, and internal forces act between the bodies. \( F_1,F_2,F_3 \) – external forces acting on bodies; \( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} \) – internal forces acting between bodies. Due to the action of forces on the bodies of the system, their impulses change. If the force does not change noticeably over a short period of time, then for each body of the system we can write the change in momentum in the form of the equation:
On the left side of each equation is the change in the momentum of the body over a short time \( \Delta t \). Let us denote: \( v_0 \) – the initial velocities of the bodies, and \( v^{\prime} \) – the final velocities of the bodies. Let's add the left and right sides of the equations.
But the interaction forces of any pair of bodies add up to zero.
Important! The momentum of a system of bodies can only be changed by external forces, and the change in the momentum of the system is proportional to the sum of the external forces and coincides with it in direction. Internal forces, changing the impulses of individual bodies of the system, do not change the total impulse of the system
Equation of motion of a rotating body
When considering this property, you should also pay attention to the equation of motion of a rotating body. Do not forget that the rotational motion of a rigid body is characterized by the presence of at least two points. Let us note the following features:
- The straight line that connects two points acts as the axis of rotation.
- It is possible to determine the location of an object in the case of calculating the rear angle between two planes.
- The most important indicator can be called angular velocity. It is related to the inertia that occurs when an object rotates.
To calculate the angular velocity, a special formula is used, which looks like this: w=df/dt. In some cases, the angular acceleration is calculated, which is also an important quantity.
Calculation of the work of elastic force
The load has made a known displacement, we also know the magnitude of the elastic force, the vectors of displacement and elastic force are parallel. It would seem that everything is clear - you need to multiply the magnitude of the force by the magnitude of the displacement and get the value of the work. However, everything is not so simple here - let's figure out why.
What does the formula that expresses the magnitude of the elastic force tell us? The fact that the elastic force is not a constant quantity, it changes as the load moves. And indeed, the magnitude of this force, as we see from the formula, depends on the coordinates of the center of the load. The formula for the work of force, which we used earlier, is valid only if the force does not change its magnitude as it moves. How then? One way out of this situation could be that we apply the same method that we used earlier in the kinematics section when calculating the displacement of a body moving with uniform acceleration.
The entire trajectory of the load can be divided into very small sections (sections within which the elastic force can be considered almost constant). Further, within each such area, we can calculate the work of the elastic force due to its practical constancy. Then the work on the entire cargo movement area will be made up of all these small works in these areas. Thus, we can calculate the work of the elastic force along the entire trajectory of the load. In Fig. 4 shows the details of such a calculation.
Rice. 4. Dependence of the elastic force on the coordinate of motion
It can be seen that if we plot on the graph the dependence of the modulus of the elastic force on the modulus of the coordinates of the load, then do the above-described division into small sections, then the amount of work in each small section is numerically equal to the area of the figure limited by the graph: the x-axis and two perpendiculars to this axis (cm Fig. 5).
Rice. 5. Area of the figure
If we sum up the value of the work in each area (the area of small figures), we obtain the area of the large figure shown in Fig. 6.
Rice. 6. Area of a large figure
Since this figure is a rectangular trapezoid, we can use the formula to calculate the area of such a figure - this is half the sum of the bases multiplied by the height. As a result of the transformations, we obtain the following formula - the work is equal to the difference between the value:
This result can be reached in a slightly different way. To calculate the work of the elastic force in this method, you simply need to take the average value of the elastic force and multiply it by the displacement of the body. This statement can be written as:
,
where is the average value of the elastic force, which is equal to half the sum of its initial and final values. If we substitute this expression into the formula for work, then using simple algebraic transformations we get the same expression that we received earlier:
As can be seen from this formula, the work depends only on the initial and final coordinates of the center of the load, and one more note: as can be seen from the last formula, the work of the elastic force in no way depends on the mass of the load. This is due to the fact that the elastic force itself does not depend on this mass.
Now let's take a closer look at the last formula - if we take -1 out of brackets, we find that the work is the difference taken with a minus sign between the values of a certain quantity, equal to half the product of the spring stiffness and the square of its elongation at the final and initial moments of time.
Let's remember what we did when calculating the work of gravity in the last lesson. That time we encountered a new physical quantity for us, the difference between the values of which at the final and initial moments of time was equal to the work of gravity taken with the “-” sign. This value is equal to the product of the mass of the body by the acceleration of gravity and the height to which the body was raised above a certain level, we called the potential energy of the body raised above the ground.