Weight determination
Weight only makes sense in a gravitational field, that is, near large objects. In other words, if a person is in the gravitational zone of a star, planet, large satellite or a decent-sized asteroid, then weight is the force that the body exerts on the obstacle between him and the source of gravity in a stationary frame of reference. This quantity is measured in newtons. Imagine that a star is hanging in space, at some distance from it there is a stone slab, and on the slab lies an iron ball. This is the force with which he presses on the obstacle, this will be the weight.
As you know, gravity depends on the distance and mass of the attracting object. That is, if the ball lies far from a heavy star or close to a small and relatively light planet, then it will act on the plate in the same way. But at different distances from the source of gravity, the resistance force of the same object will be different. What does it mean? If a person moves within one city, then nothing. But if we are talking about a climber or a submariner, then let him know: deep under the ocean, closer to the core, objects have more weight than at sea level, and high in the mountains - less. However, within our planet (by the way, not the largest even in the solar system), the difference is not so significant. It becomes noticeable when going into outer space, beyond the atmosphere.
Physical Sciences
In physics, specific weight is called weight measured per unit volume of a homogeneous substance.
Weight in the SI system is indicated in Newtons (N), and volume is calculated in cubic meters. Thus, the unit of the required characteristic becomes Newton per cubic meter (N/cub.m). It follows that this value determines the force with which one cubic meter of the measured substance acts on the support.
Physical formula: U.v. = Weight of the object, N / Volume of the object, cubic meters. m .
Unlike mass, which simply characterizes an object, weight is a vector quantity, that is, it is a force that has a direction of application and describes the effect of the body on other objects. Under normal conditions on the surface of the Earth, the difference is imperceptible to us, not physicists. We often confuse these terms in conversation and are not at all worried about it. But it is still important to understand the fundamentally different meanings these concepts have.
Read also: Fence and gates for a private house
If we use the mass of a body in the above formula, we get its specific gravity, or density. This parameter characterizes how much substance is contained in a unit volume and is measured in kg/cubic meter. m.
Body weight always remains the same, while weight can vary depending on the geographic latitude of the place and its altitude above sea level.
By representing the numerator of the fraction through the mass of the body multiplied by the acceleration of gravity, we can see the relationship between the two specific quantities:
U.V. = Object density * Gravity acceleration .
Thus, we can say that specific gravity relates to the density of a substance in the same way as its weight relates to mass, and this ratio is equal to the acceleration of gravity at a particular point on the Earth.
Determination of mass
Mass is closely related to inertia. If you go deeper, it determines what gravitational field the body creates. This physical quantity is one of the most fundamental characteristics. It depends only on matter at non-relativistic (that is, close to light) speeds. Unlike weight, mass does not depend on the distance to another object; it determines the force of interaction with it.
Also, the value of the mass of an object is invariant to the system in which it is determined. It is measured in quantities such as kilogram, ton, pound (not to be confused with foot) and even stone (which means “stone” in English). It all depends on what country a person lives in.
Determination of specific gravity
Now that the reader has understood this important difference between two similar concepts and does not confuse them with each other, we will move on to what specific gravity is. This term refers to the ratio of the weight of a substance to its volume. In the universal SI system it is denoted as newton per cubic meter. Note that the definition refers to a substance that is mentioned either in a purely theoretical (usually chemical) aspect, or in relation to homogeneous bodies.
In some problems solved in specific areas of physical knowledge, specific gravity is calculated as the following ratio: how much heavier the substance under study is than water of four degrees Celsius with equal volumes. As a rule, this approximate and relative value is used in sciences related, rather, to biology or geology. This conclusion is based on the fact that the indicated temperature is the average in the ocean across the planet. In another way, the specific gravity determined by the second method can be called relative density.
What is specific gravity
Specific gravity is understood as a vector physical quantity, defined as the ratio of the weight of a body (the weight of its substance) to the volume occupied by the body . In other words, the specific gravity is numerically equal to the product between the acceleration of gravity and the density of the substance (just in case, let us recall that the weight of a body is the force of the body on the support/suspension or its other fastening in the gravitational field).
Occasionally, a private definition unrelated to the above is also used, where specific gravity is understood as a dimensionless number indicating how many times the substance of interest is heavier than water (at its maximum density, at 4 °C) with an equal volume.
In addition to the usual everyday confusion in the form of identifying mass and weight, in relation to the case under consideration, it is necessary to mention the erroneous identification arising from the use of a similar dimension in the technical system of units of the MKGSS, where specific gravity is given as [kilogram-force / cubic meter] (kgf/m³).
Difference Between Specific Gravity and Density
The ratio that determines this quantity can easily be confused with density, since it is mass divided by volume. However, weight, as we have already found out, depends on the distance to the source of gravity and its mass, and these concepts are different. It should be noted that under certain conditions, namely at low (non-relativistic) speed, constant g and small accelerations, density and specific gravity can numerically coincide. This means that when calculating two quantities, you can get the same value for them. If the above conditions are met, such a coincidence may lead to the idea that the two concepts are one and the same. This misconception is dangerous due to the fundamental difference between the properties underlying them.
Differences between specific gravity/density
From the above it is clear that the exclusively imaginary similarity of density and specific gravity is generated by at least two factors: the general similarity in the construction of their definitions and the typical erroneous everyday identification of weight and mass. Density and specific gravity are radically different concepts.
Here are the most important differences you should know (besides the definitions):
- Specific gravity (as, indeed, any force in general) is a vector physical quantity, and density is a scalar physical quantity and characteristic of a substance.
- Density as a characteristic of a substance, ceteris paribus, is unchanged depending on the location of the measurement - and the specific gravity strongly depends even on a change in the location of the measurement location within the Earth (for example, due to variations in the acceleration of gravity between the equatorial and subpolar zones), especially if there is significant external accelerations.
- The units of measurement (in the SI/CGS systems used) are completely different in both cases: for density - [kilogram/cubic meter] or [gram/cubic centimeter], and for specific gravity - [newton/cubic meter] or [dyne/cubic centimeter ].
ScienceComment
Specific Gravity Measurement
It is difficult to obtain the specific gravity of metals and other solids at home. However, in a simple laboratory equipped with scales with deep bowls, say, in a school, this will not be difficult. A metal object is weighed under normal conditions - that is, simply in air. We will register this value as x1. Then the bowl in which the object lies is immersed in water. At the same time, according to the well-known law of Archimedes, he loses weight. The device loses its original position, the rocker arm warps. A weight is added for balancing. Let's denote its value by x2.
The specific gravity of the body will be the ratio x1 to x2. In addition to metals, specific gravity is measured for substances in various states of aggregation, at unequal pressure, temperature, and other characteristics. To determine the required value, methods of weighing, pycnometer, and hydrometer are used. In each specific case, experimental setups should be selected that take into account all factors.
Substances with the highest and lowest specific gravity
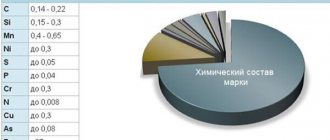
In addition to pure mathematical and physical theory, unique records are of interest. Here we will try to list those elements of the chemical system that have the highest and lowest recorded specific gravity. Among the non-ferrous metals, the heaviest are the noble platinum and gold, followed by tantalum, named after the ancient Greek hero. The first two substances have a specific gravity that is almost twice that of the following silver, molybdenum and lead. Well, the lightest among the noble metals is magnesium, which is almost six times less than the slightly heavier vanadium.
Specific gravity values of some other substances
The modern world would be impossible without iron and its various alloys, and their specific gravity undoubtedly depends on the composition. Its value varies within one or two units, but on average these are not the highest values among all substances. But what can we say about aluminum? Like its density, its specific gravity is very low - only twice that of magnesium. This is a significant advantage for the construction of high-rise buildings, for example, or aircraft, especially in combination with its properties such as strength and malleability.
Determination of specific gravity
The physical quantity, which is the ratio of the weight of a material to the volume it occupies, is called the HC of the material.
Materials science of the 21st century has gone far ahead and technologies that were considered science fiction a hundred years ago have already been mastered. This science can offer modern industry alloys that differ from each other in qualitative parameters, but also in physical and technical properties.
To determine how a certain alloy can be used for production, it is advisable to determine the HC. All objects made with the same volume, but different types of metals were used for their production, will have different masses, it is in a clear connection with volume. That is, the ratio of volume to mass is a certain constant number characteristic of this alloy.
To calculate the density of a material, a special formula is used, which has a direct connection with the HC of the material.
By the way, the HC of cast iron, the main material for creating steel alloys, can be determined by the weight of 1 cm 3, reflected in grams. The more HC the metal, the heavier the finished product will be.
Economics and Social Sciences
In economics and social sciences, the term denotes the share of a particular factor in the overall structure. This concept is of great importance, as it allows us to judge the significance of a sector, its value, and its share in the whole direction.
Formula for share in economics: U.v. = The value of an individual table column / The sum of all table columns .
In this equation, the dividend and divisor are expressed in the same units of measurement, therefore, the desired quantity will be presented as a correct decimal fraction or percentage.
Similar calculations are carried out in economics, business activity, sociology, statistics and many other disciplines that require data analysis.
When calculating, it is important to understand two things:
- The denominator of the fraction is 100%, and the sum of the indicators for all columns of the table cannot exceed it. So, if we add up the percentage shares of all budget items, we get 100%, no more and no less.
- The result of the calculation cannot be negative, because it represents a fraction of the whole.
Read also: Sharpening knives with a manual sharpener
Despite the fact that the two formulas above differ from each other and operate with different quantities, they still have something in common. In both cases, the weight of the object, its significance, influence on other objects and the situation as a whole are calculated.
Specific gravity formula
The formula for calculating HC looks like the ratio of weight to volume. To calculate hydrocarbons, it is permissible to use the calculation algorithm, which is set out in a school physics course. To do this, it is necessary to use Archimedes' law, or more precisely, the definition of the force that is buoyant. That is, a load with a certain mass and at the same time it floats on the water. In other words, it is influenced by two forces - gravity and Archimedes.
The formula for calculating the Archimedean force is as follows
F=g×V,
where g is the hydrocarbon liquid. After the substitution, the formula takes the following form: F=y×V, from here we obtain the formula for the shock load y=F/V.
Difference between weight and mass
What is the difference between weight and mass. In fact, in everyday life, it does not play any role. In fact, in the kitchen, we don't make a difference between the weight of a chicken and its mass, but there are serious differences between these terms.
This difference is clearly visible when solving problems related to the movement of bodies in interstellar space and neither those having relations with our planet, and under these conditions these terms differ significantly from each other. We can say the following, the term weight has meaning only in the zone of gravity, i.e. if a certain object is located next to a planet, star, etc. Weight can be called the force with which a body presses on the obstacle between it and the source of attraction. This force is measured in newtons. As an example, we can imagine the following picture: next to a paid education there is a stove with a certain object located on its surface. The force with which an object presses on the surface of the slab will be the weight.
Body mass is directly related to inertia. If we consider this concept in detail, we can say that mass determines the size of the gravitational field created by the body. In fact, this is one of the key characteristics of the universe. The key difference between weight and mass is this - mass does not depend on the distance between the object and the source of gravitational force.
To measure mass, many quantities are used - kilogram, pound, etc. There is an international SI system, which uses the usual kilograms, grams, etc. But besides it, many countries, for example, the British Isles, have their own system of weights and measures, where weight is measured in pounds.
What is the difference between density and volumetric weight?
⇐ PreviousPage 2 of 11Next ⇒
Density ρ is the mass of a unit volume of liquid (kg/m3): ρ = m / V,
where m – mass, kg; V – volume, m3.
The density of water at a temperature of +40C is 1000 kg/m3. Other values of water density depending on temperature can be found in the reference data. It is easy to see that the density of water depends only slightly on temperature. In most hydraulic calculations, the properties of compressibility and thermal expansion of liquids are neglected; for example, for water the density is considered constant and equal to 1000 kg/m3.
Specific gravity γ is the weight of a unit volume of liquid (N/m3): γ = G / V; where G is weight (gravity), N; V – volume, m3.
Specific gravity and density are related through the acceleration of gravity g as follows: γ = ρ g.
3.What is the relationship between the volumetric compression ratio and the volumetric modulus of elasticity? Compressibility is the property of a substance to change its volume when external pressure changes (or in other words, when stress in the substance changes). Compressibility is characterized by the volumetric compression ratio
, where V is the volume of the substance, p is the pressure. The minus sign indicates that an increase in pressure corresponds to a decrease in volume.
The above formula is incomplete because the volumetric compression ratio for any system depends on whether the process is adiabatic or isothermal. Accordingly, the isothermal volumetric compression coefficient is determined by the following formula:
, where the subscript T indicates that the partial derivative is taken at a constant temperature.
The adiabatic volumetric compression ratio is determined as follows:
, where S denotes entropy (an adiabatic process occurs at constant entropy). For solids, the differences between these two coefficients can usually be neglected. The reciprocal of the volumetric compression ratio is called volumetric modulus of elasticity , which is denoted by the letter K (in English literature - sometimes B). Sometimes the volumetric compression ratio is simply called “compressibility” .
The compressibility equation relates isothermal compressibility (and indirectly pressure) to the structure of the fluid.
Adiabatic compressibility is always less than isothermal compressibility. Fair ratio
where is the heat capacity at constant volume, is the heat capacity at constant pressure.
What is the coefficient of thermal expansion?
The coefficient of thermal expansion is a value characterizing the relative magnitude of the change in the volume or linear dimensions of a body with an increase in temperature by 1 K at constant pressure. In accordance with this, they distinguish:
⇐ Previous2Next ⇒
Recommended pages:
Difference Between Specific Gravity and Density
UV - what is it?
Specific gravity is the ratio of the weight of matter to its volume. In the SI international system of measurements it is measured as newton per cubic meter. To solve certain problems in physics, hydrocarbons are determined as follows - how much heavier the substance being examined is than water at a temperature of 4 degrees, provided that the substance and water have equal volumes.
For the most part, this definition is used in geological and biological studies. Sometimes, the HC calculated using this method is called relative density.
What are the differences
As already noted, these two terms are often confused, but since weight directly depends on the distance between the object and the gravitational source, and mass does not depend on this, therefore the terms shock wave and density differ from each other. But it is necessary to take into account that under certain conditions mass and weight may coincide. It is almost impossible to measure HC at home. But even at the school laboratory level, such an operation is quite easy to perform. The main thing is that the laboratory is equipped with scales with deep bowls.
The item must be weighed under normal conditions. The resulting value can be designated as X1, after which the bowl with the load is placed in water. In this case, in accordance with Archimedes' law, the load will lose part of its weight. In this case, the balance beam will warp. To achieve balance, a weight must be added to the other bowl. Its value can be designated as X2. As a result of these manipulations, a shock wave will be obtained, which will be expressed as the ratio of X1 and X2. In addition to substances in the solid state, specific values can also be measured for liquids and gases. In this case, measurements can be performed under different conditions, for example, at elevated ambient temperatures or low temperatures. To obtain the required data, instruments such as a pycnometer or hydrometer are used.
Volumetric weight and density
(Slide 1G3_3 )
The volumetric weight of sedimentary rock is the weight of a unit of its volume (1 cm3)
together with pores filled with liquid and gaseous phases.
The volumetric weight of a rock depends on both the mineralogical composition and the porosity of the rock, and therefore can serve as a characteristic of porosity for cemented rocks, especially when their composition is known. The volumetric weight of rocks also depends on the degree of humidity.
The most accurate volumetric weight of a rock is determined by hydrostatic weighing of a sample. The volumetric weight of the rock is calculated using the formula:
where y is the volumetric weight of the rock;
Рс is the weight of the dry sample;
Ркв is the weight of a sample saturated with kerosene in air;
Pk is the weight of the sample in kerosene;
Ak is the specific gravity of kerosene.
The accuracy of the method is ±0.02.
The volumetric weight of a completely dry rock is called the apparent, or volumetric, skeletal weight.
The volumetric weight of a rock has the same dimension and units of measurement as the specific gravity of rocks. It is usually expressed in G/cm3.
The volumetric weight of a rock is generally less than its specific gravity, but greater than the specific gravity of the liquid and gaseous phases contained in the rocks.
Due to their low porosity, the volumetric weight of minerals is almost equal to their specific gravity.
With the depth of rocks, their volumetric weight changes, usually increasing, which is associated with a decrease in rock porosity. This particularly applies to clays and clayey fine-grained sandstones and siltstones. The presence of cements characterized by high specific gravity in rocks influences the increase in bulk density.
The density of the solid (liquid, gaseous) phase is the ratio of the mass of the phase to its volume. Rock density refers to the ratio of the mass of rock with natural moisture and structure to its volume.
Bulk density is the ratio of the mass of dry rock to its volume. Density in the CGS system is expressed in g/cm.
In practice, the density of the rocks corresponds to the volumetric weight.
Porosity
(Slide 1G3_4 )
Between the solid particles that make up rocks, as a result of incomplete contact of their surfaces with each other, gaps of various sizes are formed - pores. The total volume of all pores in a unit volume, regardless of their size and filling, is called rock porosity.
The porosity of a rock is determined by the ratio of the burrow space of the rock to its total volume and is usually expressed as a percentage.
The porous space of rocks is determined not only by the size and configuration of the mineral grains that make up the rock, but also by the presence of cracks, bedding planes and the presence of cementitious substances in the pores.
The porosity of rocks can be determined by both sedimentation processes and chemical dissolution processes. In most carbonate reservoirs, which include limestones and dolomites, porosity is a consequence of the dissolution of calcite by formation waters containing dissolved carbon dioxide. The pore spaces of such rocks are usually represented by channels and caverns. Sedimentary (intergranular) porosity is determined by the presence of spaces between individual rock grains.
The porosity value of various rocks varies widely - from fractions of a percent to several tens of percent. For example, the porosity of Baku oil sands ranges from 18 to 52%, Stavropol gas-bearing siltstones and siltstones - from 30 to 40%, Volgograd oil Yasnaya Polyana sandstones - from 20 to 27%. Most often, the porosity of carbonate rocks ranges from 3-30%. The porosity of clays can reach 40-50% and higher.
Reservoir rocks of the sandy-silty type with a porosity of less than 5%, which do not contain cracks, faults and caverns, are usually of no practical importance. A.I. Levorsen (1958) gives the following approximate field estimate of rock porosity:
- negligible 0-5%,
- bad 5-10%,
— satisfactory 10-15%,
- good 15-20%,
- very good 20-25%.
However, it should be remembered that not all granulometric types of sandy-silty rocks can be assessed on this scale.
(Slide 1G3_51 )
Unlike ideal rock, the clastic grains that make up sedimentary rocks usually come in different shapes. Even well-rounded clastic grains of sandstones rarely have a regular spherical shape. The porosity of a rock consisting of spherical grains of different sizes may be higher or lower than theoretical depending on the sizes of the constituent grains.
The theoretical porosity of aggregates composed of spheres of the same diameter can range from 25.96% (Fig. 1) to 47.6% (Fig. 2). These limits coincide well with the porosity limits of sands, the porosity of which in their natural occurrence is 30-50%.
Slichter (1899) pointed out that theoretical porosity values do not depend on grain size. Thus, the porosity of gravel, consisting exclusively of grains of regular spherical shape with a diameter of 2 mm,
has the same meaning as that of clay, also composed of grains of regular spherical shape, but with a diameter of 0.05
mm.
However, in both cases the porosity is unequal: gravel is a good reservoir, and clay is practically impermeable to oil and gas.
I.M. Gubkin (1932) pointed out that the concept of “high porosity” usually implies an abundance of various holes in the rock, while the concept of “low porosity” indicates not so much the absence or insignificant number of pores, but rather the lack of pores that can accommodate and release oil . For the accumulation of oil or gas in a rock or their extraction from it, not only the relative number of pores is important, but also their absolute sizes.
Real soil grains are not spherical in shape. The presence in the rock of clayey, carbonate and other cementing substances, the grain sizes of which are smaller than the predominant sand fraction, leads to a decrease in the porosity of the sand rock. The larger the contact surface between rock grains, the lower its porosity.
The homogeneity coefficient of clastic grains of various sands in the oil-bearing regions of the USSR ranges from 1 to 20. The higher the heterogeneity coefficient, the less homogeneous the sand, the lower the porosity coefficient.
(Slide 1G3_52 )
Angular, irregularly shaped grains can be packed either more densely or more loosely than spherical ones. In this regard, they can be characterized in one case or another by both the smallest and the greatest porosity compared to ideally spherical grains. At the lowest porosity, irregularly shaped grains should have the same angular shape and, accordingly, should be stacked with offset surfaces, achieving the most dense packing. In natural conditions, a relatively loose arrangement of grains with an irregular, angular shape is quite often observed, which is reflected in the value of porosity.
The contact surface of the grains varies depending on the rock pressure, the geometric arrangement of the grains and their shape. The shape of the pore space of the rocks is more tortuous with less rounded and sorted clastic material.
Cellular and channel-shaped pores are found in limestones.
Pores close to rhomboidal and tetrahedral are often observed in rocks with well-sorted and rounded grains.
Crack-like pores are characteristic of rocks with rigid connections that have experienced tectonic forces, weathering processes, crystallization, etc.
Typically, as formation depth increases, porosity decreases. This especially applies to clayey rocks, while sandy deposits in the case of pressures that do not lead to shearing of the edges of rock grains (no more than 300 kg/cm2),
found at relatively great depths with fairly high porosity.
Total porosity is divided into macro-porosity and micro-porosity . Microporosity refers to pores less than 1 mm in size,
under macroporosity, pores are more than 1
mm.
Among the micropores, ultracapillary (subcapillary) pores with a size of less than 0.1 μm are distinguished.
The sizes of capillary pores range from 0.0002 to 0.1
mm.
Liquids in these pores move according to capillary laws, overcoming the force of gravity.
In subcapillary pores, the movement of water under the action of capillary forces is difficult or absent, since pores with a cross section of less than 0.1 μm
are completely filled with bound water (firmly connected to the pore walls) upon wetting.
Crack-like pores E.M. Smekhov (Smekhov et al., 1958) are divided into microcracks with an opening from 0.01 to 0.1 mm
and macrocracks with an opening greater than 0.1
mm;
the latter are clearly visible to the naked eye. Megapores are inherent in karst cavities of carbonate rocks.
The pore size of sandy-silty rocks varies greatly depending on the size and shape of the grains, packing density and cementation of clastic grains.
(Slide 1G3_53 )
A porous medium is characterized by a number of geometric properties:
- general porosity,
— open porosity (taking into account the volume of only interconnected pore space),
— specific internal surface and tortuosity.
A description of the concepts of types of porosity is given below.
The specific internal surface of a pore system is determined by the ratio of the internal surface of the solid phase of the rock to the containing volume and is expressed in units reciprocal to length.
The concept of tortuosity was previously introduced as a kinematic characteristic equal to the relative average length of the path traveled by a liquid particle from one side of a porous medium to the other. It is expressed in dimensionless quantities.
Some researchers (Archie, 1942; Wyllie a. Spangler, 1952, etc.) considered it possible to determine tortuosity by measuring electrical resistance, due to the fact that the current must flow through the system of capillaries that make up the pores. Based on this, we can assume that the tortuosity should be the same in the case of movement of liquid particles through the system of the same capillaries.
In addition to the above geometric properties, there is a concept about the geometric size of the pore sizes of any porous medium. However, the pore system of porous bodies forms a complex surface that is geometrically difficult to imagine.
In determining the size of pores, a convenient measure is their diameter. But an idea of the diameter is possible in the case of round pores, which is very rare. In addition, the pores, due to the fact that their walls diverge and converge, do not have a normal cross-section. Nevertheless, their size and distribution determine their approximate size.
Types of porosity
(Slide 1G3_5 )
The ratio of the volume of voids to the total volume of the rock is called porosity. However, in practice, the interconnected pore space is of greatest interest. In this regard, porosity is distinguished:
4 general, or absolute (full) - kп.abs[n, mabs, m, p]
4 open (interconnected) - kп.о [mo, me, ko]
Total porosity is understood as porosity characterized by the total volume of all voids in the rock, including pores, caverns, cracks, connected and unconnected.
Metals with the highest and lowest specific gravity
In addition to the concept of specific gravity used in mathematics and physics, there are also quite interesting facts, for example, about the specific gravities of metals from the periodic table. If we talk about non-ferrous metals, then the heaviest ones include gold and platinum.
These materials exceed in specific gravity such metals as silver, lead and many others. “Light” materials include magnesium with a weight lower than that of vanadium. We must not forget about radioactive materials, for example, the weight of uranium is 19.05 grams per cubic cm. That is, 1 cubic meter weighs 19 tons.
Specific gravity of other materials
It is difficult to imagine our world without many materials used in production and everyday life. For example, without iron and its compounds (steel alloys). The HC of these materials fluctuates in the range of one to two units and these are not the best results. Aluminum, for example, has low density and low specific gravity. These indicators allowed it to be used in the aviation and space industries.
Specific gravity of metals
Copper and its alloys have a specific gravity comparable to lead. But its compounds - brass and bronze are lighter than other materials, due to the fact that they use substances with a lower specific gravity.
Subscribe to RSS and you will receive information about site updates to your RSS channel!
Author: gidroadmin
Date of: 2008-12-08
A liquid is a continuous medium that has the property of fluidity, that is, it is capable of unlimitedly changing its shape under the influence of arbitrarily small forces, but unlike a gas, its density changes little when pressure changes.
In aeromechanics, the term “droplet liquid” is used to emphasize the difference between a liquid and a gas; the gas in these cases is called a “compressible liquid”.
Liquids can be ideal or real. Ideal - non-viscous liquids with absolute mobility, i.e. absence of frictional forces and tangential stresses and absolute immutability, and volume under the influence of external forces. Real - viscous liquids that have compressibility, resistance, tensile and shear forces and sufficient mobility, i.e. the presence of frictional forces and tangential stresses.
Real fluids can be Newtonian and non-Newtonian (Bingham). In Newtonian fluids, when one layer of fluid moves relative to another, the magnitude of the shear stress is proportional to the shear rate. At relative rest, these stresses are zero. This pattern was established by Newton in 1686, which is why these liquids (water, oil, gasoline, kerosene, glycerin, etc.) are called Newtonian liquids. Non-Newtonian fluids do not have great mobility and differ from Newtonian fluids by the presence of tangential stresses (internal friction) at rest.
Basic properties of liquids: density, specific gravity, viscosity, compressibility , etc.
Density ρ – mass of liquid per unit volume. For a homogeneous liquid
where m is the mass of liquid in volume V. The units of measurement of ρ in the CGS system are g/cm 3 , in the MKGSS system they are kgf s 2 /m 4 , and in the SI system they are kg/m 3 .
Specific gravity γ – weight of liquid per unit volume:
where G is the weight of the liquid. The units of measurement of γ in the CGS system are dyn/cm 3 , in the MKGSS system – kgf/m 3 , and in the SI system – N/m 3 .
Specific gravity and density are related by the dependence γ=ρ·g, where g is the acceleration of gravity.
Density and specific gravity of some technical fluids.
| Liquid | t, 0 C | ρ, kg/m 3 ; γ, kgf/m 3 | γ, N/m 3 | ρ, kgc s 2 /m 4 |
| Autol 10 | 20 | 920 | 9025 | 93,8 |
| Alcohol (anhydrous) | 20 | 795 | 7799 | 81,0 |
| Ammonia | -34 | 684 | 6710 | 69,7 |
| Aniline | 15 | 1004 | 9849 | 102 |
| Acetone | 15 | 790 | 7750 | 80,5 |
| Petrol | 15 | 680 – 740 | 6671 – 7259 | 69,3 – 75,4 |
| Bitumen | – | 930 – 950 | 9123 – 9320 | 94,8 – 96,8 |
| Distilled water | 4 | 1000 | 9810 | 102 |
| Sea water | 4 | 1020-1030 | 10006-10104 | 104-105 |
| Glycyrin (anhydrous) | 15 | 1270 | 11772 | 129 |
| Tar | 15 | 930-950 | 9123-9320 | 94,8-96,8 |
| Coal tar | 15 | 1200 | 12459 | 122 |
| Kerosene | 15 | 790 – 820 | 7750-8044 | 80,5 – 93,5 |
| Fuel oil | 15 | 890 – 940 | 8731 – 9221 | 90,7 – 95,8 |
| Oil: | ||||
| -vaseline | 20 | 860 – 890 | 8437 – 8731 | 87,7 – 90,7 |
| -industrial 12 | 20 | 876 – 891 | 8594 – 8741 | 89,3 – 90,8 |
| -industrial 20 | 20 | 881 – 901 | 8643 – 8839 | 89,8 – 93,3 |
| -industrial 30 | 20 | 886 – 916 | 8692 – 8986 | 90,3 – 93,4 |
| -industrial 45 and 50 | 20 | 890 – 930 | 8731 – 9123 | 90,7 – 94,8 |
| -industrial 45 and 50 | 20 | 890 – 930 | 8731 – 9123 | 90,7 – 94,8 |
| -castor | 20 | 960 | 9418 | 97,8 |
| -machine | 20 | 898 | 8809 | 91,5 |
| -transformer | 20 | 887 – 896 | 8701 – 8790 | 90,4 – 91,3 |
| -turbine 30 and 32 | 20 | 894 – 904 | 8770 – 8868 | 91,1 – 92,1 |
| Whole milk | 20 | 1029 | 10094 | 103 |
| Natural oil | 15 | 700 – 900 | 6867 – 8829 | 71,4 – 91,7 |
| Beer | 15 | 1040 | 10202 | 106 |
| Mercury | 20 | 13546 | 132886 | 1381 |
| Methyl alcohol | 15 | 810 | 7946 | 82,6 |
| Ethanol | 15-18 | 790 | 7750 | 80,5 |
| Molten cast iron | 17 | 1210 | 11870 | 123 |
Read also: How to connect wires to a two-key switch
Density of water and mercury at different temperatures.
Source: Vilner Ya.M. Reference manual on hydraulics, hydraulic machines and hydraulic drives.
Views: 164260
Comments on this article!!
Comment added by: mqsqt Date: 2011-09-03
Comment added by: Bashtag Date: 2012-10-29
Comment added by: Sanya Date: 2013-11-12
Comment added by: Ir Date: 2014-01-15
Comment added by: ir Date: 2014-04-28
Comment added by: lelik Date: 2014-10-20
Nice way to go
Comment added by: sens Date: 2014-10-23
Thank you very much for the table. It was very useful. ))))
Comment added by: Yuri Date: 2014-12-30
Comment added by: edld Date: 2015-01-28
Comment added by: Vitaly Date: 2018-05-14
Thank you very much for the material
Add your comment
| Similar articles! | |
| Viscosity of liquids | Viscosity of water, milk, gasoline, oil, alcohol | |
| Hydrostatic pressure. Pascal's law. | |
| Bernoulli's equation - the basic equation of hydraulics | |
| Compressibility of liquids | |
| Laminar and turbulent fluid flow regime | |
| The most popular articles on the site! | |
| Conversion of units of measurements. Pressure unit converter | |
| Viscosity of liquids | Viscosity of water, milk, gasoline, oil, alcohol | |
| Density and specific gravity of liquids | Density of water, oil, alcohol, kerosene, gasoline and petroleum | |
| Hydraulic calculation of pipelines | |
| Bernoulli's equation - the basic equation of hydraulics | |
| Laminar and turbulent fluid flow regime | |
| Hydrostatic pressure. Pascal's law. | |
| Thermal expansion of liquids | |
| Compressibility of liquids | |
| History of hydraulics. History of the development of hydraulics. Part 1. From ancient Greece to the mid-18th century. | |
VIDEO COURSE Your First DSLR
8 sections on all aspects of photography; 73 video lessons ; 6 hours 31 minutes of the best materials; 5.7 GB of material on a dual-layer DVD;
Site administration: E-mail - hover your mouse here You can send your wishes, suggestions and comments to improve the site using this form @2008-2019 When using site materials, a link to the site is required!