Потенциальная энергия пружины: понятие, закон сохранения, уравнение

Понятие потенциальной энергии пружины

При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:

Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.

Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.

Вычисление работы силы упругости

Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.

О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.

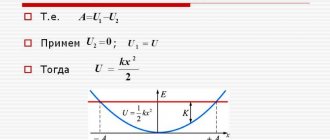
Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.

Рис. 4. Зависимость силы упругости от координаты движения

Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).

Рис. 5. Площадь фигуры

Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.

Рис. 6. Площадь большой фигуры

Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:

К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:

где среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:

Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.

Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.

Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.

Закон сохранения механической энергии

Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.

Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.

Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.

Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.

Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.

Постигаем закон Гука

Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.

Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину \( x \), потребуется приложить внешнюю силу \( F_{вн} \), которая равна:

где \( k \) — это коэффициент пропорциональности.

Точнее говоря, вектор деформации \( \mathbf{x} \) всегда направлен противоположно силе сопротивления пружины (или силе упругости) \( \mathbf{F} \), а потому в векторную формулировку закона Гука обычно входит знак “минус”:

Растягиваем и сжимаем пружины

Следует помнить, что закон Гука относится только к упруго деформируемым материалам.

В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности \( k \) в законе Гука \( F=kx \) называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.

Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?

Вес автомобиля равен \( mg \), где \( g \) — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка \( mg/4 \).

Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:

т.е. коэффициент упругости равен:

Подставляя значения, получим:

Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·103 Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.

Изучаем особенности закона Гука

Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:

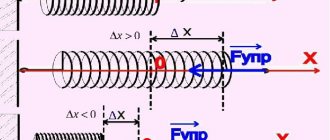
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.

Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).

Сила упругости пружины не зря называется силой сопротивления, ведь она стремится установить равновесие.

Динамика твердого тела

Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела

Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.

Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.

Средняя кинетическая энергия

Кинетическая энергия представляет собой энергию, определяемую скоростью движения разных точек, которые принадлежат этой системе. Однако следует помнить, что необходимо различать 2 энергии, характеризующие разные виды движения: поступательное и вращательное. Средняя кинетическая энергия (СКЭ) при этом является средней разностью между совокупностью энергий всей системы и ее энергией спокойствия, то есть, по сути, ее величина — это средняя величина потенциальной энергии. Формула средней кинетической энергии следующая:

где k — это константа Больцмана; Т — температура. Именно это уравнение является основой молекулярно-кинетической теории.

Момент силы и момент импульса относительно оси

Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.

Момент импульса – величина, которая применяется для определения количества вращательного движения.

Среди особенностей подобного показателя можно отметить следующее:

Масса вращения. Объект может характеризоваться различной массой.
Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.

Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.

Импульс системы тел

Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.

Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы. \( F_1,F_2,F_3 \) – внешние силы, действующие на тела; \( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} \) – внутренние силы, действующие между телами. Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:

В левой части каждого уравнения стоит изменение импульса тела за малое время \( \Delta t \). Обозначим: \( v_0 \) – начальные скорости тел, а \( v^{\prime} \) – конечные скорости тел. Сложим левые и правые части уравнений.

Но силы взаимодействия любой пары тел в сумме дают нуль.

Важно! Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы

Уравнение движения вращающегося тела

Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:

Прямая, которая соединяет две точки, выступает в качестве оси вращения.
Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.

Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.

Вычисление работы силы упругости

Рис. 4. Зависимость силы упругости от координаты движения

Рис. 5. Площадь фигуры

Рис. 6. Площадь большой фигуры