Spring pendulum - formulas and equations for finding quantities

A spring pendulum is an oscillatory system that consists of a body suspended from a spring. This system is capable of free oscillations.

Such systems are quite widespread due to their functional flexibility. Mechanisms based on such pendulums are often used as elements of automation equipment.

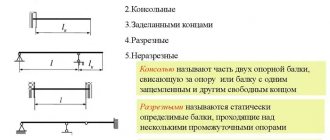
Among other things, they have found application in contact fuses of various ammunition, and as accelerometers in missile control circuits. They are also actively used in safety valves installed in pipelines.

Energy concept

Before considering the features of a spring, you should pay attention to what happens to it during compression, stretching and how it affects the body surrounding the system.
Energy is a scalar physical quantity that is used to determine the form of motion and interaction of matter. An important point is that if the system is closed, then the force is maintained over a long period. Today it surrounds us almost everywhere and touches quite a large number of objects.

The concept of kinetic energy of a spring has become quite widespread. It is connected with the direct features of the product itself. When a certain force is applied to the turns located along one spiral, a force is generated that can be used as useful work.

Types of spring pendulums

There are two types of this system:

1. Vertical

   pendulum - the body is quite strongly influenced by gravity. This influence causes an increase in the inertial movements that the body makes at the starting point.

2. Horizontal

   - in this case, when moving, a frictional force begins to act on the load, which arises due to the fact that the load lies on the surface.

Energy concept

To operate the engines that propel cars, tractors, diesel locomotives, and airplanes, fuel is needed, which is a source of energy. Electric motors power machine tools using electricity. Due to the energy of water falling from a height, hydraulic turbines are turned, connected to electrical machines that produce electric current. In order to exist and work, a person also needs energy. They say that in order to do any work, energy is needed. What is energy?

• Observation 1. Let's raise the ball above the ground. While he is in a state of calm, no mechanical work is performed. Let's let him go. Under the influence of gravity, the ball falls to the ground from a certain height. As the ball falls, mechanical work is performed.
• Observation 2. Close the spring, fix it with a thread and place a weight on the spring. Let's set fire to the thread, the spring will straighten and raise the weight to a certain height. The spring has done the mechanical work.
• Observation 3. We attach a rod with a block at the end to the cart. We will throw a thread through the block, one end of which is wound around the axle of the cart, and a weight hangs on the other. Let's release the weight. Under the influence of gravity, it will fall down and give the cart movement. The weight did the mechanical work.

After analyzing all the above observations, we can conclude that if a body or several bodies perform mechanical work during interaction, then they are said to have mechanical energy, or energy.

Problems on the topic with detailed solutions

Problem 1

An airplane weighing 50 tons flies at an altitude of 10 kilometers. The speed of the vehicle is 900 km/h. You need to calculate what the total mechanical energy of the aircraft is.

Solution

The first step is to translate the required data according to the SI system. In this case, the mass of the aircraft will be 50,000 kg, the speed will be 250 m/s, and the height will be 10,000 m.

The aircraft has a reserve of total energy, which includes both potential and kinetic.

E = Ep + Ek

Ep = m * g * h

Ek = m * v2 / 2

Thus, the total energy will be:

\(E=m\times g\times h\times \frac{mv^{2}}{2}\)

If we substitute the numerical values ​​of the quantities from the problem conditions into the resulting formula, we obtain the total energy:

\(E=6.5625\times 10^{9}\) J

If we write down the answer in abbreviation, it will take the following form:

\(E = 6.5625\) GJ.

Answer: in the considered frame of reference, the value of the total mechanical energy of the aircraft will be 6.5625 GJ.

However, this problem can be solved by taking the 10-kilometer mark as the zero level. Then the vehicle will be characterized only by its reserve of kinetic energy, and the value of potential energy will be equal to zero.

Problem 2

The spring was secured to the wall and placed on a smooth surface. A body was fixed at the end of the spring. Tension of a spring, which has a stiffness of 400 N/m, occurs when a force of 80 N is applied. It is necessary to calculate the energy reserve in the spring.

Solution

According to the conditions of the problem, the surface is smooth, which allows us to conclude that the friction force is zero. Thus, energy losses are eliminated. By acting on the spring, you can observe its deformation. The entire supply of energy will be concentrated in it. This value can be found using the formula:

\(E=\frac{k(\Delta x)^{2}}{2}\)

The elastic force is equal to the product of the stiffness and the change in the length of the spring:

\(k\times \Delta x=F\)

The spring deformation can be calculated as follows:

\(\Delta x=\frac{F}{k}\)

Using the last equality, you can transform the formula for calculating energy:

\(E=\frac{k(\frac{F}{k})^{2}}{2}=\frac{kF^{2}}{2k^{2}}=\frac{F^{ 2}}{2k}\)

Next, you should substitute the numerical values ​​into the resulting expression:

\(E=\frac{80^{2}}{2\times 400}=8\) J

Answer: The energy reserve in the spring is 8 J.

Problem 3

The bullet weight is 9 grams. She was fired from the weapon vertically in an upward direction. The bullet speed was 700 m/s. It is required to calculate its kinetic energy.

Solution

It is convenient to present the conditions of the problem in the form of a picture.

The calculation must be performed using the formula:

\(E=\frac{mv^{2}}{2}\)

Before you can substitute numerical values ​​into the equation, you need to convert them to the SI system. Then the mass of the bullet will be 0.009 kg. The expression will be written as follows:

\(E=\frac{0.009\times 49\times 10^{4}}{2}=2200\) J

Answer: the reserve of kinetic energy of a bullet is 2200 J.

Problem 4

The mass of the rocket is 0.2 kg. She was fired from the gun vertically upward. After this, the rocket reached a height of 60 meters. It is required to calculate the value of the potential energy of the rocket characteristic of this mark.

Solution

The condition of the problem can be represented using a picture.

In order to calculate potential energy, you need to use the formula:

E = m * g * h

Next, you need to substitute numerical values ​​into the expression:

E = 0.2 * 9.8 * 60 = 118 J

Answer: The potential energy of the rocket at a given altitude will be 118 J.

Problem 5

The spring was stretched by 5 mm. Its rigidity coefficient is 10,000 N/m. You need to calculate what the energy of the spring is.

Solution

The conditions of the problem should be presented in the figure.

The equation that can be used to calculate the spring energy is:

\(E=\frac{k(\Delta x)^{2}}{2}\)

Next, you need to convert the distance over which the spring was stretched to the SI system. It will be 0.005 m.

After the transformations, you can substitute the numerical values ​​into the desired formula:

\(E=\frac{10^{4}\times 25\times 10^{-6}}{2}=0.125\) J

Answer: The spring energy is 0.125 J.

Knowledge of the basic formulas for calculating the kinetic, potential and total energy of a body will allow you to solve problems of any complexity. The simplest way is to perform sequential actions, including writing down the conditions of the problem, graphically depicting the system, presenting formulas for calculating energy, solving the equation by substituting numerical values

It is important to note that mechanical energy is the sum of potential and kinetic energy

Examples of problems on finding kinetic energy

1. Compare the kinetic energy of a ball weighing 9 g flying at a speed of 300 m/s and a person weighing 60 kg running at a speed of 18 km/h.

So, what we are given: m1 = 0.009 kg; V1 = 300 m/s; m2 = 60 kg, V2 = 5 m/s.

Solution:

• Kinetic energy (formula): Ek = mv2:2.
• We have all the data for the calculation, and therefore we will find Ek for both the person and the ball.
• Ek1 = (0.009 kg x (300 m/s)2): 2 = 405 J;
• Ek2 = (60 kg x (5 m/s)2): 2 = 750 J.
• Ek1 < Ek2.

Answer: the kinetic energy of the ball is less than that of a person.

2. A body with a mass of 10 kg was raised to a height of 10 m, after which it was released. What FE will it have at a height of 5 m? Air resistance can be neglected.

So, what we are given: m = 10 kg; h = 10 m; h1 = 5 m; g = 9.81 N/kg. Ek1 - ?

Solution:

• A body of a certain mass, raised to a certain height, has potential energy: Ep = mgh. If a body falls, then it will have sweat at a certain height h1. energy Ep = mgh1 and kin. energy Ek1. In order to correctly find the kinetic energy, the formula given above will not help, and therefore we will solve the problem using the following algorithm.
• In this step, we use the law of conservation of energy and write: En1 + Ek1 = En.
• Then Ek1 = Ep - Ep1 = mgh - mgh1 = mg(h-h1).
• Substituting our values ​​into the formula, we get: Ek1 = 10 x 9.81(10-5) = 490.5 J.

Answer: Ek1 = 490.5 J.

3. A flywheel with mass m and radius R rotates around an axis passing through its center. The angular speed of rotation of the flywheel is ω. In order to stop the flywheel, a brake pad is pressed against its rim, acting on it with a frictional force F. How many revolutions will the flywheel make before it comes to a complete stop? Take into account that the mass of the flywheel is concentrated along the rim.

So, what we are given: m; R; ω; Friction. N — ?

Solution:

• When solving the problem, we will consider the revolutions of the flywheel to be similar to the revolutions of a thin homogeneous hoop with radius R and mass m, which rotates with angular velocity ω.
• The kinetic energy of such a body is equal to: Ek = (Jω2) : 2, where J = mR2.
• The flywheel will stop provided that all of its FE is spent on overcoming the frictional force Ffriction arising between the brake pad and the rim: Ek = Ffriction*s, where s is the braking distance, which is equal to 2πRN.
• Consequently, Ffriction*2πRN= (mR2ω2) : 2, whence N = (mω2R) : (4πFtr).

Answer: N = (mω2R) : (4πFtr).

Change in kinetic energy

The above information indicates that the value in question is not a constant indicator. Among the features we note:

1. The greatest value is characterized by the maximum elongation of the turns relative to each other. At the same time, we should not forget that there is a certain limitation regarding the maximum elongation, since too much load causes deformation.
2. As the body approaches the equilibrium point, it decreases. This is due to the fact that the elasticity index is significantly reduced.

In addition, the parameter depends on the influence of other forces. An example is friction, which reduces the speed of an object.

Period and frequency of free oscillations of a spring pendulum

When developing projects, the period of oscillation and its frequency are always determined. To measure them, formulas known in physics are used.

The change in cyclic frequency will be shown by the formula shown in the figure:

Factors on which frequency depends:

1. Elasticity coefficient.

   This coefficient is affected by the number of turns, their diameter, the distance between them, the length of the spring, the stiffness of the alloy used, etc.

2. Cargo weight.

   The resulting inertia and speed of movement depend on this factor.

Calculation of the work of elastic force

The load has made a known displacement, we also know the magnitude of the elastic force, the vectors of displacement and elastic force are parallel. It would seem that everything is clear - you need to multiply the magnitude of the force by the magnitude of the displacement and get the value of the work. However, everything is not so simple here - let's figure out why.

What does the formula that expresses the magnitude of the elastic force tell us? The fact that the elastic force is not a constant quantity, it changes as the load moves. And indeed, the magnitude of this force, as we see from the formula, depends on the coordinates of the center of the load. The formula for the work of force, which we used earlier, is valid only if the force does not change its magnitude as it moves. How then? One way out of this situation could be that we apply the same method that we used earlier in the kinematics section when calculating the displacement of a body moving with uniform acceleration.

The entire trajectory of the load can be divided into very small sections (sections within which the elastic force can be considered almost constant). Further, within each such area, we can calculate the work of the elastic force due to its practical constancy. Then the work on the entire cargo movement area will be made up of all these small works in these areas. Thus, we can calculate the work of the elastic force along the entire trajectory of the load. In Fig. 4 shows the details of such a calculation.

Rice. 4. Dependence of the elastic force on the coordinate of motion

It can be seen that if we plot on the graph the dependence of the modulus of the elastic force on the modulus of the coordinates of the load, then do the above-described division into small sections, then the amount of work in each small section is numerically equal to the area of ​​the figure limited by the graph: the x-axis and two perpendiculars to this axis (cm Fig. 5).

Rice. 5. Area of ​​the figure

If we sum up the value of the work in each area (the area of ​​small figures), we obtain the area of ​​the large figure shown in Fig. 6.

Rice. 6. Area of ​​a large figure

Since this figure is a rectangular trapezoid, we can use the formula to calculate the area of ​​such a figure - this is half the sum of the bases multiplied by the height. As a result of the transformations, we obtain the following formula - the work is equal to the difference between the value:

This result can be reached in a slightly different way. To calculate the work of the elastic force in this method, you simply need to take the average value of the elastic force and multiply it by the displacement of the body. This statement can be written as:

,

where is the average value of the elastic force, which is equal to half the sum of its initial and final values. If we substitute this expression into the formula for work, then using simple algebraic transformations we get the same expression that we received earlier:

As can be seen from this formula, the work depends only on the initial and final coordinates of the center of the load, and one more note: as can be seen from the last formula, the work of the elastic force in no way depends on the mass of the load. This is due to the fact that the elastic force itself does not depend on this mass.

Now let's take a closer look at the last formula - if we take -1 out of brackets, we find that the work is the difference taken with a minus sign between the values ​​of a certain quantity, equal to half the product of the spring stiffness and the square of its elongation at the final and initial moments of time.

Let's remember what we did when calculating the work of gravity in the last lesson. That time we encountered a new physical quantity for us, the difference between the values ​​of which at the final and initial moments of time was equal to the work of gravity taken with the “-” sign. This value is equal to the product of the mass of the body by the acceleration of gravity and the height to which the body was raised above a certain level, we called the potential energy of the body raised above the ground.

Elastic force in a spring pendulum

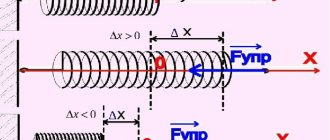
Before deformation begins, the spring is in an equilibrium state. The applied force can either stretch or compress it.

By applying the law of conservation of energy to a spring pendulum, we can calculate the elastic force in it. Elasticity is directly proportional to the distance over which the load has shifted.

The elastic force can be calculated as follows:

F control
= - k*x
where k is the spring stiffness coefficient (N\m),

x – displacement (m).

Features of kinetic energy during rotation

Let's compare the formula for kinetic energy during rotation with the formula for the kinetic energy of a body for linear motion:

$$E_k ={v^2 m \over 2}$$

You can see their closeness. But, in the formula for rotation for a material point there is an additional factor - radius. Its necessity is explained by the fact that when rotating through the same angle, a material point located at a farther distance from the center of rotation travels a longer distance compared to a closer point. Therefore, its instantaneous linear speed, and therefore its kinetic energy, is greater. For solids of various shapes, the radius of rotation is also taken into account when determining the moment of inertia.

It is easy to verify that a material point with a large radius of rotation has greater kinetic energy by unwinding a load on a cord. If you untwist the load at a constant frequency (say, one revolution per second), then with a short length of the cord this is easy to do, however, the longer the cord, the more effort you have to apply, although the mass of the cord remains constant.

That's why you can throw a stone further with a sling than just with your hand. A larger radius of rotation allows you to impart more energy to the stone.

Rice. 3. Throwing a stone using a sling.

Answers

Simple mechanisms. Efficiency of simple mechanisms →

← Mechanical work. Power

Potential and kinetic energy. Law of conservation of mechanical energy

2.9 (58.06%) 31 votes

Question 5

Question text

The capacitor of the oscillating circuit is charged from a constant voltage source and then connected to coils with different inductances: L 1, L 2, L 3. Select words in the second column of the table that correctly characterize changes in the parameters of harmonic oscillations in the oscillating circuit when the inductance of the coils decreases in such experiments

Read also: How to resharpen a chain for rip sawing

For each quantity, determine the corresponding nature of the change:

Write down the selected numbers for each physical quantity in the table. The numbers in the answer may be repeated.

Kinetic energy - concept and definition

Definition

Kinetic energy is the ability of a moving body to do a certain amount of work.

For example, a moving car can demolish an obstacle in front of it, and a falling stone can leave a dent on a metal plate.

Kinetic energy depends on the speed of movement and body mass. It is described by the formula:

\(E_k=\frac{m\nu^2}2\)

The unit of kinetic energy is Joule (J).

By carrying out simple transformations, it is easy to derive formulas for calculating body mass and speed of movement:

\(m=\frac{2E_k}{\nu^2}\)

\(\nu=\sqrt{\frac{2E_k}m}\)

From the basic formula it is clear: the number of times the body mass changes, the number of times the kinetic energy changes. For example, if the mass is reduced or increased by 5 times, then the amount of kinetic energy will become correspondingly smaller or larger by 5 times.

As speed increases, kinetic energy increases quadratically. Let’s say the speed of the body’s movement has become 6 times greater. Accordingly, its kinetic energy increased 36 times.

The formula for the kinetic energy of a body is valid only for speeds significantly lower than the speed of light. If the speed of movement approaches 300,000 km/s, then the theory of relativity, created by Albert Einstein, comes into play.

Kinetic energy depends on the considerations of the system. If the body is accepted as a macroscopic object, then it will have internal energy. In this case, kinetic energy will arise only at the moment of its movement.

The same body can also be viewed from a microscopic point of view. The thermal movement of atoms and molecules determines the internal energy of the body. At the same time, the average kinetic energy of this movement is proportional to the absolute temperature of the body. The coefficient of this proportional dependence is called Boltzmann's constant.

The kinetic energy of atoms and molecules when considering a body at a microscopic level is described by the formula:

\(E_k=\frac32kT\)

where \(k\) is Boltzmann's constant.

Kinetic energy: formula and definition

Sometimes the meaning of mechanical work can be considered without using the concepts of force and displacement, focusing on the fact that work characterizes a change in the energy of the body. All we need is the mass of a certain body and its initial and final speed, which will lead us to kinetic energy. Kinetic energy (KE) is the energy possessed by a body due to its own motion.

Wind has kinetic energy and is used to propel wind turbines. The moving masses of air exert pressure on the inclined planes of the wings of wind turbines and force them to turn around. Rotational motion is transmitted through gear systems to mechanisms that perform specific work. The moving water that circulates around the turbines of a power plant loses some of its CE as it performs work. An airplane flying high in the sky, in addition to PE, has CE. If a body is at rest, that is, its speed relative to the Earth is zero, then its CE relative to the Earth is zero. It has been experimentally established that the greater the mass of a body and the speed at which it moves, the greater its CE. The formula for kinetic energy of translational motion in mathematical expression is as follows:

Where K is kinetic energy, m is body mass, v is speed.

Work and potential energy of a body raised above the Earth

The amount of potential energy depends on the choice of the zero energy level. In the Earth's gravitational field, a body located on the surface of the planet has a zero energy level.

Work of gravity

The work done by gravity is equal to the change in the potential energy of the body, taken with the opposite sign:

A = – ∆Ep = –(mgh – mgh) = mg(h – h)

If a body rises, gravity does negative work. If a body falls, gravity does positive work.

Example No. 3. A ball weighing 100 g rolled down a hill 2 m long, making an angle of 30° with the horizontal. Determine the work done by gravity.

First, let's convert the units of measurement to SI: 100 g = 0.1 kg. Under the influence of gravity, the position of the body relative to the Earth has changed by an amount equal to the height of the slide. We can find the height of the slide by multiplying its length by the sine of the angle of inclination. The initial height is equal to the height of the slide, the final height is zero. From here:

A = mg(h – h) = 0.1∙10(2∙sin30o – 0) =2∙0.5 = 1 (J)

Potential energy of an extended body

Work of gravity

The potential energy of an extended body is expressed through its center of mass. For example, to lift a crowbar with length l and mass m, you need to do work equal to:

A = mgh

where h is the height of the center of mass of the scrap above the Earth's surface. Since the crowbar is uniform along its entire length, its center of mass will be located midway between its ends, or:

Hence the work that needs to be done to lift this crowbar will be equal to:

Example No. 4. The student lifted a 0.5 m long ruler lying on the table by one end so that it was in a vertical position. What is the minimum amount of work done by the student if the mass of the ruler is 40 g?

Let's convert the units of measurement to SI: 40 g = 0.04 kg. The minimum work required to lift a ruler at one end is:

Work and change in potential energy of an elastically deformed body

Recall that work is determined by the formula:

A = Fscosα

When we compress the spring, the ball moves in the same direction as the traction force. If we stretch it, the ball also moves in the direction of the traction force. Therefore, the elastic force vector and the displacement vector are co-directed, therefore, the angle between them is zero, and its cosine is one:

The modulus of the traction force is equal in modulus to the elastic force, therefore:

The movement is determined by the formula:

s = x – x

Therefore, the work done by the traction force to compress or stretch the spring is equal to:

But it is known that the potential energy of an elastically deformed body is equal to:

Consequently, the work done by the force under the influence of which the spring is stretched or compressed is equal to the change in its potential energy:

Maximum kinetic energy of load

For a simple spring pendulum, the total energy of the load at any time can be expressed as

• $E_p$ is potential energy,
• $E_k$ is kinetic energy,
• $m$ — mass,
• $v$ — instantaneous speed,
• $k$ is the elasticity coefficient,
• $x$ is the increment in the length of the spring at the moment.

Ask a question to the experts and get an answer within 15 minutes!

The maximum kinetic energy can be calculated as

where $v_$ is the maximum speed of the load. However, it is difficult to measure in practice. It is easier, based on the constancy of the sum of kinetic and potential energies, to determine the maximum potential (when the kinetic is zero). Since the converse is also true, we can write:

where $x_$ is the maximum increment in spring extension. It is easy to measure, and the elasticity coefficient can be found in a reference book.

A compact weight weighing 0.5 kg is attached to a spring moving horizontally. Its coefficient of elasticity is 2000 $frac $. What was the initial increment in the length of the spring if its maximum speed during oscillation is 1 $frac $?

From the conditions of the problem, you can find the maximum kinetic energy of the load:

Expressing the maximum potential energy in terms of the increment in the length of the spring, we create the equality:

Answer: $approx 1.6 mm$.

Still haven't found the answer to your question?

Just write what you need help with

The weight of a mathematical pendulum with a mass of 10 g performs harmonic oscillations. In this case, the speed v of the load changes over time t according to the law v = 2sin ( 0.5πt )

What is the maximum kinetic energy of the load during such vibrations?

please help - I know E kin = mv^2/2 but where should I get the values ​​from. what to take from this formula? ( v = 2sin ( 0.5πt )) 2 is the speed that can be substituted into E? 0.5 is w, what can I do about it?

OU. I didn't get 0.02. Soooo. and in what units is this? is this equal to 2m j?

With free mechanical vibrations, kinetic and potential energies change periodically. At the maximum deviation of a body from its equilibrium position, its speed, and therefore its kinetic energy, vanish. In this position, the potential energy of the oscillating body reaches its maximum value. For a load on a horizontal spring, potential energy is the energy of elastic deformation of the spring. For a mathematical pendulum, this is energy in the Earth’s gravitational field.

When a body in its motion passes through the equilibrium position, its speed is maximum. At this moment it has maximum kinetic and minimum potential energy. An increase in kinetic energy occurs due to a decrease in potential energy. With further movement, potential energy begins to increase due to a decrease in kinetic energy, etc.

Thus, during harmonic oscillations, a periodic transformation of kinetic energy into potential energy and vice versa occurs.

If there is no friction in the oscillatory system, then the total mechanical energy during free oscillations remains unchanged.

Equations of oscillations of a spring pendulum

Free oscillations of a spring pendulum are described using the harmonic law.

If we assume the probability that the oscillations occur along the X axis, and Hooke’s law is satisfied, then the equation will take the form:

F(t) = ma(t) = — mw2x(t),

where w is the radial frequency of the harmonic vibration.

To calculate vibrations, taking into account all probabilities, the following formulas are used:

Moment of force and moment of impulse about the axis

The deformation of the spring is also considered taking into account the moment of force and momentum relative to the axis. These two parameters allow you to calculate all the required indicators with higher accuracy. A fairly common question is what the moment of force is - a vector quantity that is determined by the vector product of the radius and the vector of the applied force.

Momentum is a quantity that is used to determine the amount of rotational motion.

Among the features of this indicator are the following:

1. Rotation mass. An object can have different masses.
2. Distribution relative to the axis. The axis can be located at different distances from the object itself.
3. Rotational speed. This property is considered the most important; depending on the design, it can be constant or change.

The calculation of each indicator is carried out by applying the appropriate formula. In some cases, the required input data is measured, without which calculations will not be possible.

Elastic deformations are a source of energy

If a weight is attached to a spring with stiffness k on a horizontal surface, the spring is pulled out, and then the weight is released, then under the action of the elastic force of the spring the weight will begin to move and move a certain distance. Let's try again to calculate the work that the elastic force does when the spring lengthens from the initial position x1 to the final position x2.

Rice. 3. Potential energy of the spring:.

The elastic force will vary depending on the size of the deformation. The work done by the elastic force Fу when the spring is displaced from point x1 to point x2 will be equal to:

$A = F_у (x_1 – x_2)$ (10).

According to Hooke's law, the elastic force is directly proportional to the deformation of the spring, and its average value is:

$F_{usr} = k*{ (x_1 + x_2)\over 2}$ (11).

Substituting in (10) instead of Fу the value from equation (11), we obtain:

$A = k*{ (x_1 + x_2)\over 2} *(x_1 – x_2)= {k *( x_1^2 – x_2^2)\over 2}$ (12).

Equation (12) can be presented in a slightly different form:

$A = {k*x_1^2\over 2} – { k*x_2^2\over 2}$ (13).

From equation (13) it is clear that the work is equal to the difference in the magnitude of the potential energy Ep at points x1 and x2:

$Ep = {k*x^2\over 2}$ (14),

From equations (13) and (14) it follows that the work of the elastic force is equal to the change in the potential energy of the spring. If at the end point x2=0, i.e. the spring is not deformed, then:

$Ep = A$ (15).

This means that the potential energy of a deformed body is equal to the work done by the elastic force during the transition of the body to a state with zero deformation.

The reason for the emergence of elastic forces lies in the interaction of atoms and molecules of the body. When compressed, repulsive forces arise between atoms, and when stretched, attractive forces arise, which tend to restore the initial dimensions. Atoms and molecules contain electrons and protons - particles with electrical charges. As a result of deformations, the relative positions of atoms and molecules change. Electric forces tend to return atoms to their original position. This is how elastic force arises.

The elastic moduli of various bodies are calculated using special mathematical models based on experimental data. The values ​​of elastic moduli for various materials are given in reference tables.

Oscillations of a load on a spring - a lesson. Physics, 9th grade

A mechanical oscillatory system consisting of a spring with a coefficient of elasticity (stiffness) (k), one end of which is rigidly fixed, and on the other there is a mass load (m), is called a spring pendulum.

Let's consider the simplest spring pendulum - a rigid body (load) moving along a horizontal plane, attached by a spring to the wall. Let us assume that friction forces do not have a significant effect on the movement of the load.

Initially, the spring is not deformed (neither stretched nor compressed), so no forces in the horizontal direction act on the load. Point O is the equilibrium position of the load.

• Let's move the load to the right. At the same time, the spring will stretch, and an elastic force will arise in it, directed to the left, towards the equilibrium position, and in modulus equal to:
• Fcontrol=kx=kA,
• where (x=A) is the maximum (amplitude) deviation of the load from the equilibrium position.

If you release the load, then under the action of the elastic force it will begin to accelerate to the left, to point (O), as it approaches which the speed of the load will increase from zero to a certain maximum value. In this case, the elastic force will decrease. Having reached the equilibrium position, the load will continue to move to the left.

When the load moves from point (O) to the left, the spring will compress. An elastic force will again arise in it, which in this case will be directed towards the equilibrium position, that is, to the right, against the speed of movement of the load, and it will slow down the movement of the load. As a result, the load will stop at the leftmost point.

But the elastic force directed to point (O) will continue to act, so the load will again begin to move in the opposite direction, to the right, and on the way back its speed will increase from zero to the maximum value at point (O).

The movement of the load from point (O) to the extreme right point will again lead to stretching of the spring, again an elastic force will arise, directed towards the equilibrium position and slowing down the movement of the load until it stops completely.

Thus, the load will make one complete oscillation. In this case, at each point of its trajectory (except for point (O)), it will be acted upon by the elastic force of the spring directed towards the equilibrium position.

1. Newton's second law for such a system, provided there are no external forces and friction forces, has the form:
2. ma=−kx, from where
3. a=−kmx is the acceleration of the spring pendulum.

Law of conservation of mechanical energy

According to established laws, the mechanical effect of a conservative mechanical system is maintained over time. This moment determines that the potential energy of a deformed spring cannot arise on its own or disappear somewhere. That is why you need to make an appropriate effort to create it.

The law under consideration belongs to the category of integral equalities. This pattern determines that it is the result of the action of differential laws and is a property or sign of the cumulative impact.

To carry out the corresponding calculations, a certain formula must be applied. The force with which the impact is exerted is not constant. That is why the graphical method is used to calculate it. The simplest relationship can be described as follows: F=kx. When applying such a dependence, the constructed coordinate line will be represented by a straight line, which is located at an angle relative to the coordinate system.

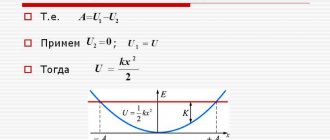
Potential energy can be attributed to such a device only if it is equal to the maximum work and does not depend on the conditional trajectory of movement. Conducted studies indicate that such work obeys Hooke's law. To determine the main indicator, the following formula is used: U=kk2/2.

To deform the turns, a certain force must be applied to them, since otherwise the kinetic force will not arise.

Average kinetic energy of gas molecules

Numerous experiments have established that the average kinetic energy of gas molecules in translational motion at a given temperature is the same and does not depend on the type of gas. In addition, it was also found that when the gas is heated by 1 °C, the SCE increases by the same value. To be more precise, this value is equal to: ΔEk = 2.07 x 10-23 J/oC. In order to calculate what the average kinetic energy of gas molecules in translational motion is, it is necessary, in addition to this relative value, to know at least one more absolute value of the energy of translational motion. In physics, these values ​​are quite accurately determined for a wide range of temperatures. For example, at a temperature t = 500 oC, the kinetic energy of the translational motion of a molecule Ek = 1600 x 10-23 J. Knowing 2 quantities (ΔEk and Ek), we can both calculate the energy of translational motion of molecules at a given temperature, and solve the inverse problem - determine the temperature from given energy values.

Finally, we can conclude that the average kinetic energy of molecules, the formula of which is given above, depends only on the absolute temperature (and for any state of aggregation of substances).