Что такое механические свойства?
Механические свойства алюминия, как и других материалов – это свойства, которые связаны с упругой и неупругой реакцией материала на приложение к нему нагрузки, в том числе, зависимость между напряжениями и деформациями. Примерами механических свойств являются:
- модуль упругости (при растяжении, при сжатии, при сдвиге)
- предел прочности (при растяжении, при сжатии, при сдвиге)
- предел текучести
- предел усталости
- удлинение (относительное) при разрыве
- твердость.
Механические свойства часто ошибочно относят к физическими свойствам.
Механические свойства материалов, в том числе, алюминия и его сплавов, которые получают путем испытания материала на растяжение, например, модуль упругости при растяжении, прочность при растяжении, предел текучести при растяжении и относительное удлинение называют механическими свойствами при растяжении.
Механические свойства алюминия
Что такое механические свойства?
Механические свойства алюминия, как и других материалов – это свойства, которые связаны с упругой и неупругой реакцией материала на приложение к нему нагрузки, в том числе, зависимость между напряжениями и деформациями. Примерами механических свойств являются:
- модуль упругости (при растяжении, при сжатии, при сдвиге)
- предел прочности (при растяжении, при сжатии, при сдвиге)
- предел текучести
- предел усталости
- удлинение (относительное) при разрыве
- твердость.
Механические свойства часто ошибочно относят к физическими свойствам.
Механические свойства материалов, в том числе, алюминия и его сплавов, которые получают путем испытания материала на растяжение, например, модуль упругости при растяжении, прочность при растяжении, предел текучести при растяжении и относительное удлинение называют механическими свойствами при растяжении.
Модуль упругости
Модуль упругости, который часто называют модулем Юнга – это отношение напряжения, которое приложено к материалу, к соответствующей деформации в том интервале, когда они являются прямо пропорциональными друг к другу.
Различают три типа напряжений и соответственно три типа модулей упругости для любого материала, в том числе для алюминия:
- модуль упругости при растяжении
- модуль упругости при сжатии
- модуль упругости при сдвиге (сдвиговый модуль упругости).
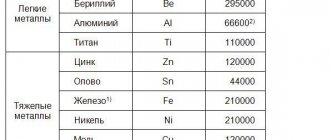
Таблица — Модули упругости при растяжении алюминия и других металлов [1]
Прочность при растяжении
Отношение максимальной нагрузки перед разрушением образца при испытании его на растяжение на исходную площадь поперечного сечения образца. Также применяются термины «предел прочности при растяжении» и «временное сопротивление разрыву».
Предел текучести
Напряжение, которое необходимо для достижения заданной малой пластической деформации в алюминии или другом материале при одноосной растягивающей или сжимающей нагрузке.
Если пластическая деформация под воздействием растягивающей нагрузки задается как 0,2 %, то применяется термин «предел текучести 0,2 %» (Rp0,2).
Рисунок — Типичная диаграмма напряжение-деформация для алюминиевых сплавов
Удлинение (при разрыве)
Часто называется «относительным удлинением». Увеличение расстояния между двумя метками на испытательном образце, которое возникает в результате деформирования образца при растяжении до разрыва между этими метками.
Величина удлинения зависит от размеров поперечного сечения образца. Например, величина удлинения, которая получена при испытании алюминиевого листового образца будет ниже для тонкого листа, чем для толстого листа. Тоже самое относится и к прессованным алюминиевым профилям.
Удлинение А
Удлинение в процентах после разрыва образца при исходном расстоянии между метками 5,65 · √ S0, где S0 – исходная площадь поперечного сечения испытательного образца. Устаревшее обозначение этой величины А5 в настоящее время не применяется. Аналогичная величина в русскоязычных документах обозначается δ5.
Легко проверить, что для круглых образцов это расстояние между исходными метками вычисляется как 5·d.
Удлинение А50мм
Удлинение в процентах после разрыва образца по отношению к исходной длине между метками 50 мм и постоянной исходной ширине испытательного образца (обычно 12,5 мм). В США применяется расстояние между метками в 2 дюйма, то есть 50,8 мм.
Сдвиговая прочность
Максимальное удельное напряжение, то есть максимальная нагрузка, разделенная на исходную площадь поперечного сечения, которую выдерживает материал при испытании на сдвиг. Сдвиговая прочность обычно составляет 60 % от прочности при растяжении.
Сдвиговая прочность является важной характеристикой качества заклепок, в том числе, алюминиевых.
Коэффициент Пуассона
Отношение между продольным удлинением и поперечным сокращением сечения при одноосном испытании. Для алюминия и всех алюминиевых сплавов во всех состояниях коэффициент Пуассона обычно составляет 0,33 [2].
Твердость
Сопротивление металла пластическому деформации, обычно измеряемое путем отпечатка.
Твердость Бринелля (HB)
Сопротивление проникновению сферического индентора при стандартизированных условиях.
Для алюминия и алюминиевых сплавов твердость НВ приблизительно равна 0,3·Rm, где Rm
– предел прочности при растяжении, выраженный в МПа [2].
Если применяется индентор из карбида вольфрама, то применяется обозначение HBW.
Твердость Викерса (HV)
Сопротивление проникновению алмазного индентора в виде квадратной пирамиды при стандартизированных условиях. Твердость HV приблизительно равна 1,10·HB [2].
Усталость
Тенденция металла разрушаться при длительных циклическом напряжении, которое значительно ниже предела прочности при растяжении.
Усталостная прочность
Максимальная амплитуда напряжения, которую может выдерживать изделие при заданном количестве циклов нагружения. Обычно выражается как амплитуда напряжения, которая дает 50%-ную вероятность разрушения после заданного количества циклов нагружения [2].
Усталостная выносливость
Предельное напряжение, ниже которого материал будет выдерживать заданного количество циклов напряжения [2].
Механические свойства алюминия и алюминиевых сплавов
В таблицах ниже [3] представлены типичные механические свойства алюминия и алюминиевых сплавов:
- предел прочности при растяжении
- предел текучести при растяжении
- удлинение при растяжении
- усталостная выносливость
- твердость
- модуль упругости
Механические свойства представлены отдельно:
- для алюминиевых сплавов, упрочняемых нагартовкой.
- для алюминиевых сплавов, упрочняемые термической обработкой.
Эти механические свойства — типичные. Это означает, что они годятся только для сравнительных целей, а не для инженерных расчетов. В большинстве случаев они являются средними значениями для различных размеров изделий, их форм и методов изготовления.
Источник:
- Материалы Алюминиевой ассоциации Германии
- Global Advisory Group GAG – Guidance «Terms and Definitions» – 2011-01
- Aluminium and Aluminium Alloys. — ASM International, 1993.
aluminium-guide.ru
Модуль упругости
Модуль упругости, который часто называют модулем Юнга – это отношение напряжения, которое приложено к материалу, к соответствующей деформации в том интервале, когда они являются прямо пропорциональными друг к другу.
Различают три типа напряжений и соответственно три типа модулей упругости для любого материала, в том числе для алюминия:
- модуль упругости при растяжении
- модуль упругости при сжатии
- модуль упругости при сдвиге (сдвиговый модуль упругости).
Таблица – Модули упругости при растяжении алюминия и других металлов [1]
Определение модуля упругости и коэффициента Пуассона
0. ВВЕДЕНИЕ
В методических указаниях к лабораторной работе N 3 «Определение модуля упругости и коэффициента Пуассона» указывается цель работы, приводится характеристика испытуемого образца и даётся методика проведения испытаний.
Для лучшего усвоения материала по темам: «Растяжение и сжатие» и «Упруго – механические свойства материалов» приводятся основные теоретические положения, позволяющие квалифицированно провести испытания, экспериментально определить по одному испытанию образца величины упругих постоянных (Е и μ) и проанализировать полученные результаты.
Завершаются методические указания перечнем возможных вопросов при защите отчета по этой лабораторной работе.
2. ЦЕЛЬ РАБОТЫ
Определить опытным путем величину модуля упругости Ε и коэффициент Пуассона μ и сравнить полученные результаты со справочными данными.
3. ОБОРУДОВАНИЕ, ПРИБОРЫ И ИНСТРУМЕНТЫ
Испытательная машина – МР-0,5. Тензометрическая станция – ЦТМ-5. Штангенциркуль.
4. ХАРАКТЕРИСТИКА ОБРАЗЦОВ
Вид образца, имеющего прямоугольное поперечное сечение, представлен на рис.1. На больших сторонах поперечного сечения образца наклеены по одному тензодатчику в продольном направлении и по одному в поперечном. Каждый тензодатчик подключен к отдельному каналу тензометрической станции ЦТМ-5.
Рис. 1. Вид обра о тензо датчиками
5. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
При деформациях подавляющего большинства материалов в упругой стадии справедлив закон Гука, который устанавливает прямую пропорциональную зависимость между напряжениями и деформациями:
σ = Ε·ε (1)
Величина Ε представляет собой коэффициент пропорциональности и называется модулем упругости первого рода. Так как относительное удлинение – величина безразмерная, модуль упругости Ε имеет размерность напряжения. Закон Гука справедлив при напряжениях, не превышающих предел пропорциональности апц.
На диаграмме растяжения (сжатия) (рис.2) модуль упругости Ε представлен тангенсом угла наклона прямой О А к оси (tg α).
Рис.2. Диаграмма растяжения ( сжатия ) образца из малоуглеродистой стали:
- растяжения,
- сжатия
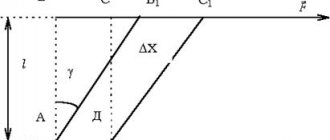
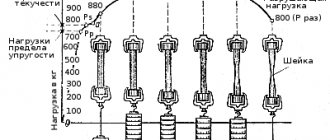
При растяжении стержня, его удлинение в продольном направлении сопровождается пропорциональным сужением в поперечном направлении, что показано на рис.3.
Рис.3. Изменение формы образца при испытаниях на растяжение
Продольную деформацию принято обозначать: абсолютную – Δi (Δ^ = i\- l),
относительную -ε (ε = Δ -£ / ^). Поперечную деформацию обозначим:
абсолютную – ДЬ (Ab = bi – b),
относительную – ε1 (ε1 = Ab / b). Как показывает опыт ε’= – μ · ε,
где μ – безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона, величина которого зависит только от материала и характеризует его свойства. Знак » – » указывает, что продольная и поперечная деформации всегда противоположны по знаку. Коэффициент Пуассона принято считать положительной величиной, поэтому относительные линейные деформации берутся по абсолютной величине (μ= ε11 /1 ε |).
6. ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ
1. Перед испытанием студентам необходимо ознакомиться с устройством машины МР-0,5 ( первое занятие ) и правилами поведения в лаборатории при проведении испытаний (вводный инструктаж ).
2. Измеряют штангенциркулем характерные линейные размеры испытуемого образца.
3. Убеждаются в подключении тензодатчиков к тензометрической станции ЦТМ-5.
4. Наблюдают за включением машины, процессом нагружения образца начальной нагрузкой (0 – 100 Η ), которая задается преподавателем.
5. Путем последовательного переключения соответствующих каналов тензометрической станции снимают показания каждого из тензометров. Эти данные заносятся в журнал наблюдений. В отчете по лабораторной работе в разделе «Результаты испытаний» предварительно готовится таблица..
6. Наблюдают за последующими двумя ступенями нагружения (100 – 200 Η каждая по указанию преподавателя ) образца, снимают показания тензодатчиков и заносят их в таблицу.
7. В процессе проведения испытаний внимательно следят за комментариями преподавателя и при завершении испытаний по его указанию приступают к обработке результатов испытания.
7. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ
В журнале наблюдений ( табл. ) подсчитываются приращения соответствующих отсчетов и определяются их средние значения (АсрР, АсрАь АсрА2, ДсрВь АсрВ2). Затем подсчитываются средние приращения по тензометрам в продольном (АсрА) и поперечном (АсрВ) направлениях.
По найденным АсрА и АсрВ находятся значения относительной линейной деформации соответственно в продольном и поперечном направлениях:
ε = АсрА · с , ε1 = АсрВ · с ,
где с – коэффициент чувствительности тензодатчика, который определяется тарировкой и сообщается преподавателем.
Определяются значение нормального напряжеия, средин для каждой ступени нагружения образца:
σ = АсрР / F, где F – площадь поперечного сечения образца ( F = b · d).
Исходя из закона Гука при растяжении – сжатии (σ= Ε-ε) находится модуль упругости материала образца:
Ε = σ/ε.
По найденным значениям относительных деформаций в продольном и поперечном направлениях определяется величина коэффициента Пуассона:
μ=Η/Ιε|.
Для любого материала величина коэффициента Пуассона должна находиться в пределах от 0 до 0,5.
Найденные значения модуля упругости Ε и коэффициента Пуассона μ следует сравнить с соответствующими величинами, приведенными в справочной литературе и сделать выводы.
Предел текучести
Напряжение, которое необходимо для достижения заданной малой пластической деформации в алюминии или другом материале при одноосной растягивающей или сжимающей нагрузке.
Если пластическая деформация под воздействием растягивающей нагрузки задается как 0,2 %, то применяется термин «предел текучести 0,2 %» (Rp0,2).
Рисунок 4 – Типичная диаграмма напряжение-деформация для алюминиевых сплавов
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. | ||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
| Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. | ||||
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость | |||
| Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 | ||
Удлинение (при разрыве)
Часто называется «относительным удлинением». Увеличение расстояния между двумя метками на испытательном образце, которое возникает в результате деформирования образца при растяжении до разрыва между этими метками.
Величина удлинения зависит от размеров поперечного сечения образца. Например, величина удлинения, которая получена при испытании алюминиевого листового образца будет ниже для тонкого листа, чем для толстого листа. Тоже самое относится и к прессованным алюминиевым профилям.
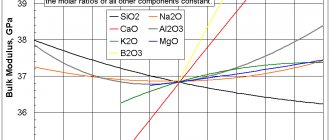
Рисунок 5 – Влияние легирующих элементов на прочностные свойства и относительное удлинение [4]
Удлинение А
Удлинение в процентах после разрыва образца при исходном расстоянии между метками 5,65 · √ S0, где S0 – исходная площадь поперечного сечения испытательного образца. Устаревшее обозначение этой величины А5 в настоящее время не применяется. Аналогичная величина в русскоязычных документах обозначается δ5.
Легко проверить, что для круглых образцов это расстояние между исходными метками вычисляется как 5·d.
Удлинение А50мм
Удлинение в процентах после разрыва образца по отношению к исходной длине между метками 50 мм и постоянной исходной ширине испытательного образца (обычно 12,5 мм). В США применяется расстояние между метками в 2 дюйма, то есть 50,8 мм.
Модуль упругости. Коэффициент Пуассона
Вопрос об определении нормальных напряжений теснейшим образом связан с расчетами бруса на прочность. Умение вычислять деформации и перемещения необходимо для расчетов на жесткость, а также для определения сил в статически неопределимых системах.
Выделим из бруса, изображенного на рис. 17.7 бесконечно малый элемент длиной dz
.
Отношение приращения (изменения) длины элемента к его первоначальной длине называется относительным удлинением или продольной деформацией:
(17.2)
Очевидно, продольная деформация – безразмерная величина. В некоторых случаях ее выражают в процентах. При растяжении продольную деформацию считают положительной, а при сжатии – отрицательной.
Отношение изменения размера поперечного сечения к его первоначальному значению называют относительным поперечным сужением (расширением), или поперечной деформацией:
(17.3)
Продольную и поперечную деформации называют также линейными деформациями.
В известных пределах нагружения между (деформацией) и соответствующим (действующим в ее направлении) напряжением существует прямо пропорциональная (линейная) зависимость.
Это положение носит название закона Гука и записывается в виде
(17.4)
Коэффициент пропорциональности E называют модулем продольной упругости (модуль упругости 1-го рода; модуль Юнга). Е имеет ту же размерность, что и напряжение, т.е. выражается в Па или МПа.
Модуль продольной упругости – физическая постоянная данного материала, характеризующая его жесткость. Чем жестче материал, тем меньше он деформируется при данном напряжении.
Опытным путем установлено, что при простом растяжении или сжатии отношение поперечной деформации к продольной – величина постоянная для данного материала. Это отношение, взятое по абсолютному значению, называется коэффициентом поперечной деформации, или коэффициентом Пуассона;
(17.5)
Значения коэффициента Пуассона для различных материалов находятся в пределах от 0 до 0.5.
Минимальное значение коэффициент Пуассона имеет для пробки ( = 0); максимальное – для каучука ( 0.5). Для большинства металлов и сплавов значение коэффициента Пуассона колеблется в сравнительно узких пределах: от 0.23 до 0.35 (в среднем примерно 0.3).
Вопрос об определении изменения длины (удлинения или укорочения) бруса. Удлинение или укорочение равно:
(17.6)
Выражение (17.6) часто называют формулой Гука, а произведение Е∙А условно называют жесткостью сечения бруса при растяжении (сжатии).
Понятие жесткости бруса (участка бруса)определяется по формуле
(17.7)
Жесткость бруса численно равна силе, вызывающей удлинение (или укорочение) бруса, равное единице длины: 1 м или 1 см и т.п.
При расчетах в единицах СИ коэффициент жесткости выражают в ньютонах на метр (Н/м).
Величину, обратную коэффициенту жесткости, называют коэффициентом податливости:
(17.8)
Коэффициент податливости численно равен удлинению (укорочению) бруса, вызванному силой, равной единице силы: 1 H или 1 кН.
(17.9)
или
(17.10)
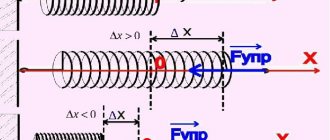
17.4. Частный случай плоского напряженного состояния – чистый сдвиг. Закон Гука при сдвиге.
Рассмотрим частный случай плоскогонапряженного состояния, для которого отличные от нуля главные напряжения равны по модулю и противоположны по знаку (рис. 17.8).
Такое напряженное состояние носит название чистого сдвига. Максимальное главное напряжение следует обозначить , минимальное ; по условию, ; промежуточное главное напряжение = 0.
Чистым сдвигом называют такое плоское напряженное состояние, при котором в окрестности данной точки можно выделить элемент таким образом, чтобы на четырех его гранях были только равные между собой касательные напряжения.
В качестве примера, иллюстрирующего возникновение чистого сдвига, рассмотрим кручение тонкостенной трубы (рис. 17.9 а). Из условия равновесия отсеченной части трубы, изображенной отдельно на рис. 17.9 б, следует, что в поперечном сечении (любом) возникает лишь один внутренний силовой фактор – крутящий момент , численно равный
внешнему моменту М. В поперечном сечении трубы возникают касательные напряжения ( ).
Деформация сдвига. Изобразим элемент, выделенный площадками, на которых возникают только касательные напряжения. Учитывая, что нас интересуют деформации элемента, а не его перемещения как твердого тела, будем считать одну из граней неподвижной. Мерой деформации сдвига служит изменение первоначального прямого угла между гранями элемента, называемое углом сдвига и обозначаемое . Угол сдвига, выражается в радианах (рис. 17.10).
Между углом сдвига и соответствующим касательным напряжением существует прямая пропорциональность – закон Гука при сдвиге.
(17.11)
Здесь G –
упругая постоянная материала, характеризующая его
жесткость при деформации сдвига и называемая модулем сдвига или модулем упругости 2-го рода. Размерность модуля сдвига та же, что и напряжения.
(17.12)
Сдвиговая прочность
Максимальное удельное напряжение, то есть максимальная нагрузка, разделенная на исходную площадь поперечного сечения, которую выдерживает материал при испытании на сдвиг. Сдвиговая прочность обычно составляет около 60 % от прочности при растяжении.
Сдвиговая прочность является важной характеристикой качества заклепок, в том числе, алюминиевых.
Рисунок 6 – Прочность на сжатие, прочность на сдвиг, несущая прочность и твердость различных алюминиевых сплавов [4]
Твердость
Сопротивление металла пластическому деформации, обычно измеряемое путем отпечатка.
Твердость Бринелля (HB)
Сопротивление проникновению сферического индентора при стандартизированных условиях.
Для алюминия и алюминиевых сплавов твердость НВ приблизительно равна 0,3·Rm, где Rm – предел прочности при растяжении, выраженный в МПа [2].
Если применяется индентор из карбида вольфрама, то применяется обозначение HBW.
Твердость Викерса (HV)
Сопротивление проникновению алмазного индентора в виде квадратной пирамиды при стандартизированных условиях. Твердость HV приблизительно равна 1,10·HB [2].
Механические свойства алюминиевых сплавов
Прочность на смятие алюминиевых сплавов
Прочность на смятие алюминия также трудно определять, испытывать и связывать с обычными прочностными свойствами, как и для других металлов. Смятие часто является важным критерием для конструкций с применением соединений на заклепках и болтах и поэтому «прочность на смятие» является широко признанной характеристикой. Прочность на смятие весьма произвольно определяют как давление (на единицу эффективной площади смятия), прилагаемое шпилькой в круглом отверстии. Это отверстие предварительно раздают на 2 % от исходного диаметра (рисунок 1). Эта прочность для большинства алюминиевых сплавов составляет 1,8 от прочности при растяжении (временного сопротивления) (рисунок 2).
Рисунок 1
Рисунок 2
Прочность на срез алюминиевых сплавов
Схема нагружения при испытании на срез приведена на рисунке 3. Для деформируемых алюминиевых сплавов отношение прочности на срез к прочности при растяжении различается в зависимости от химического состава и метода изготовления от 0,5 до 0,75 (см. рисунок 2). В случае отсутствия данных по прочности на срез ее обычно принимают 0,55 от прочности при растяжении.
Рисунок 3
Заклепки из марок алюминия и сплавов Al—Mn (серия 3ххх) изготовляют методами холодной деформации с достижением прочности на срез до 200 МПа. Заклепки из термически упрочняемых сплавов изготовляют в отожженном состоянии, затем сразу подвергают закалке и естественному старению с достижением прочности на срез до 260 МПа.
Сопротивление материала местной пластической деформации, возникающей при внедрении в него более твердого тела – индентора — является приблизительным индикатором состояния сплава и поэтому широко применяется при контроле продукции. Для алюминиевых сплавов применяют методы Бринелля (стальной шарик), Викерса (алмазная пирамидка) и Шора (падающий алмазный конус). Твердость по Бринеллю изменяется от 20 единиц для чистого алюминия до 175 единиц для термически упрочненного сплава 7075 (см. рисунок 2). По показаниям твердости, как правило, не вычисляют их прочность при растяжении, как это обычно делают для сталей, так как для алюминиевых сплавов соотношение этих двух характеристик далеко от постоянного.
Усталость
Тенденция металла разрушаться при длительных циклическом напряжении, которое значительно ниже предела прочности при растяжении.
Рисунок 7 – Различие в усталостном поведении низкоуглеродистой стали иалюминиевых сплавов [3]
Усталостная прочность
Максимальная амплитуда напряжения, которую может выдерживать изделие при заданном количестве циклов нагружения. Обычно выражается как амплитуда напряжения, которая дает 50%-ную вероятность разрушения после заданного количества циклов нагружения [2].
Усталостная выносливость
Предельное напряжение, ниже которого материал будет выдерживать заданного количество циклов напряжения [2].