Крутильные колебания модуль кручения и модуль сдвига

Если один конец длинного однородного стержня закрепить, а к другому приложить закручивающий момент сил М

, то этот конец повернется на угол , причем, согласно закона Гука:

. (1)

Постоянная величина носит название модуля кручения. Модуль кручения связан с модулем сдвига материала стержня G

соотношением:

, (2)

где r

– радиус, а
L
– длина стержня. Отметим, что простая линейная зависимость между величинами
М
и , даваемая формулой (1), имеет место только при сравнительно небольших значениях
М
. В общем случае зависимость может быть не только нелинейной, но и неоднозначной.

I. Определение модуля кручения стержня статическим методом

Принадлежности: исследуемый стержень, отсчетная труба со шкалой, рулетка, микрометр, набор грузов.

Экспериментальная установка изображена на рис.1. верхний конец вертикального стержня С

жестко закреплен на стойке, а нижний соединен с диском
Д
. Момент
М
, закручивающий стержень, создают две навитые на диск и перекинутые через блоки
Б
нити, к концам которых подвешиваются одинаковые грузы
Г
. Диск снабжен зеркальцем
З
. Для определения угла закручивания стержня надо зрительную трубу направить на зеркальце и добиться того, чтобы в нее было видно отражение шкалы, укрепленной на том же штативе, что и труба. Наблюдая через трубу за смещением видимого участка шкалы при закручивании стержня, можно определить угол закручивания .

Рис.1. Схема установки для

определения модуля кручения

Измерения

1. Установите зрительную трубу таким образом, чтобы в нее было четко видно отражение шкалы в зеркальце З

   .

2. Увеличивая нагрузку на нитях Н

   , снимите зависимость . Проделайте эксперимент в обратном порядке, постепенно уменьшая величину закручивающего момента. Весь комплекс измерений проделайте не менее трех раз.

3. Результаты эксперимента изобразите графически в координатах . При помощи этих графиков определите величину ƒ и оцените допущенную при этом погрешность.
4. Используя формулу (2), вычислите модуль сдвига G

   . Сверьте полученное таким образом значение с табличным.

II. Определение модуля сдвига при помощи крутильных колебаний

Принадлежности: проволока из исследуемого материала, грузы, секундомер, микрометр, рулетка, масштабная линейка.

Экспериментальная установка состоит из длинной вертикально висящей проволоки, к нижнему концу которой прикреплен горизонтальный металлический стержень с двумя симметрично расположенными грузами. Их положение на стержне можно фиксировать.

Верхний конец проволоки зажат в цангу и при помощи специального приспособления вместе с цангой может проворачиваться вокруг вертикальной оси. Таким образом в системе можно возбудить крутильные колебания. Запишем для этого случая уравнение движения:

. (3)

Здесь М

– момент сил, обязанный своим происхождением упругим деформациям,
J
– момент инерции стержня с грузами, — угол поворота стержня.

Если амплитуда колебаний невелика, то для определения момента сил М

можно воспользоваться законом Гука в форме (1). Момент
М
в этом случае вызван деформацией проволоки и стремиться уменьшить, а не увеличить угол . В формуле (1) необходимо поэтому переменить знак. После подстановки (1) формула (3) приобретет вид:

. (4)

; отсюда:

, (5)

где амплитуда и фаза определяются начальными условиями. Таким образом, является угловой частотой крутильных колебаний стержня, период Т

которых равен:

. (6)

Следует заметить, что последняя формула получена для незатухающих колебаний, в то время как на самом деле колебания стержня затухают. Если, однако, затухание невелико, т.е. изменение амплитуды колебаний за период много меньше самой амплитуды, то формулой (6) можно пользоваться. Критерием ее применимости служит неравенство:

п

> > 1, (7)

где п

– число полных колебаний, после которого амплитуда уменьшается в 2-3 раза.

Отметим, что период Т

, как видно из формулы (6), не зависит от амплитуды . Однако при больших амплитудах закон Гука нарушается, и такая зависимость может проявиться. Таким образом, вторым условием применимости описываемого метода является соблюдение равенства:

T = const

. (8)

Кручение

Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.

Пример деформации кручения цилиндрического стержня

Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).

Рис. 1.

Отношение угла закручивания φ к длине называют относительным углом закручивания

Закон Гука для малых деформаций кручения выражается формулой

M = Gкр.j

где Gкр.– модуль кручения.

Модуль кручения , помимо материала, зависит также от формы и размеров тела.

Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.

Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

Рис. 2.

Деформация кручения является частным случаем деформации сдвига.

Сдвиг

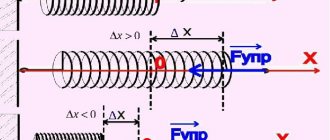
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.

Так как угол мал, формулу можно записать в виде:

где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.

τ = F / S = Gg

где G — модуль сдвига.

Закон Гука для малой деформации сдвига выражается формулой:

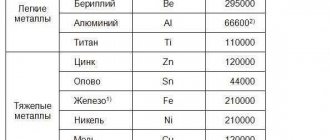
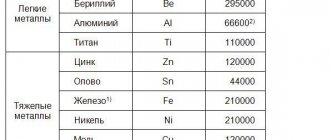
Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра.

Измерения

1. Прежде всего установите диапазон амплитуд, в котором выполняется условие (8). Для этого укрепите грузы на некотором расстоянии от проволоки и возбудите в системе крутильные колебания. Измеряя время нескольких (не менее 10-ти) полных колебаний, найдите период Т1

   . уменьшая амплитуду вдвое, тем же способом найдите соответствующий период
   Т2
   . если
   Т1= Т2
   , то для проведения измерений можно выбрать любую амплитуду не больше первой. Если же окажется, что , то амплитуду необходимо уменьшить до такого значения , начиная с которого для всех < будет справедливо равенство
   Т1= Т2
   .

2. Проверьте справедливость неравенства (7).
3. Установив грузы так, чтобы их центры масс находились на некотором расстоянии L1

   от оси системы, измерьте период, как описано выше. Если
   J
   – момент инерции без грузов, а
   J1
   – момент инерции грузов, то, очевидно:

. (9)

Изменив расстояние грузов до величины L2

, аналогично получим:

. (10)

Из (9) и (10) следует:

,

где 2т

– масса двух грузов. Масса одного груза 550 г.

Определение величины ƒ

проведите для нескольких (не менее 5-ти) пар значений
L1
и
L2
. величину
ƒ
можно также найти из наклона прямой в графике, по осям которого отложены
L2
и
Т2
. разработка этого вопроса предоставляется читателю.

1. Зная ƒ

   , найдите значение модуля сдвига
   G
   по формуле (2) и оцените допущенную при этом погрешность.

Примеры

• Пусть M
  — свободный модуль над кольцом
  R
  , из определения немедленно следует, что
  M
  является модулем без кручения. В частности, векторные пространства не имеют кручения.
• В модулярной группе любой нетривиальный элемент кручения либо имеет порядок 2 и является сопряженным с S
  , либо имеет порядок 3 и является сопряжённым с
  ST
  . Элементы кручения здесь не образуют подгруппу: например,
  S
  ·
  ST
  =
  T
  , а
  T
  имеет бесконечный порядок.
• Абелева группа Q / Z {\displaystyle \mathbb {Q} /\mathbb {Z} } (которую можно представлять себе как группу поворотов окружности на угол, соизмеримый с длиной окружности) является группой кручения. Этот пример можно обобщить следующим образом: если R
  — коммутативное кольцо, а
  Q
  — его поле частных, то
  Q/R
  является группой кручения.
• Пусть задано векторное пространство V
  над полем
  F
  с линейным оператором. Если естественным образом рассматривать это пространство как
  F(x)
  -модуль, то этот модуль является модулем кручения (по теореме Гамильтона-Кэли, или просто из-за того, что пространство конечномерно).

Контрольные вопросы

1. Выведите формулу (2).
2. При определении модуля сдвига статическим способом зависимость рекомендуется снять как при возрастающих, так и при убывающих значениях М

   . Почему? Совпадут ли оба полученные таким образом результаты, если трение в осях блоков
   Б
   будет значительным?

3. При определении модуля сдвига динамическим способом указывалось, что период колебаний не зависит от амплитуды только при сравнительно небольших значениях последней. Объясните качественно, как будет меняться период при возрастании амплитуды?
4. Какому методу определения G

   вы отдадите предпочтение на практике, статическому или динамическому?

5. Как при динамическом определении G

   измерить величины
   L1
   и
   L2
   ? Имеет ли смысл выбирать их малыми?

6. Как оценить ошибку измерений по графику зависимости Т2

   от
   L2
   ?

Кручение в гомологической алгебре

Понятие кручения играет важную роль в гомологической алгебре. Если M

и
N
— модули над коммутативным кольцом
R
, функтор Tor позволяет получить семейство
R
-модулей Tor
i
(
M
,
N
). При этом модуль
S
-кручения модуля
M
естественно изоморфен Tor1(
M
,
RS
/
R
). В частности, из этого сразу следует, что плоские модули являются модулями без кручения. Название
Tor
является сокращением от английского
torsion
(кручение).

Ис­пытание образца на кручение с определением модуля сдвига

Ι. ВВЕДЕНИЕ

В методических указаниях к лабораторной работе N 4 » Ис­пытание образца на кручение с определением модуля сдвига» ука­зывается цель работы, приводится характеристика испытуемого образца и дается методика проведения испытаний. Для лучшего усвоения материала по теме «Кручение» приводятся основные тео­ретические положения, позволяющие квалифицированно провести испытания, определить величину модуля сдвига и проанализиро­вать полученные результаты испытания.

Завершаются методические указания перечнем возможных вопросов при защите отчета по этой лабораторной работе.

2. ЦЕЛЬ РАБОТЫ

Определить опытным путем величину модуля сдвига (G), сравнить полученное значение со справочным для данного мате­риала и проверить справедливость закона Гука при данном испыта­нии.

3. ОБОРУДОВАНИЕ, ПРИБОРЫ И ИНСТРУМЕНТЫ

Испытательная машина – КМ-50 Индикатор часового типа Штангенциркуль Мерительная линейка.

4. ХАРАКТЕРИСТИКА ОБРАЗЦА

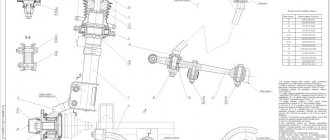
Вид испытуемого образца представлен на рис.1. Головки образца, предназначенные для крепления в захватах машины KiVI-50, изготовлены из сплошного материала и присоединены к телу образца с помощью сварки. На головках образца имеются лыски, исключающие прокручивание их в захватах машины. Мате­риал образца – сталь ст.З.

Рис.1. Вид испытуемого образца:

1 – тело образца,

2 – головка образца,

3 – сварной шов

5. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

При сдвиге в упругой стадии (рис. 2) справедлив закон Гука, который устанавливает прямую пропорциональную зависимость между касательным напряжением (τ) и углом сдвига (γ):

τ= G · γ

Величина G представляет собой коэффициент пропорцио­нальности и называется модулем упругости второго рода или моду­лем сдвига. Закон Гука справедлив при напряжениях не

превышающих предел пропорциональности – Тпц.

Рис. 2. Деформация сдвига

При кручении стержня круглого сечения его элементы на­ходятся в состоянии чистого сдвига (рис.3).

Учитывая, что при кручении напряжения – τ зависят от кру­тящего момента Μ , а угол закручивания – φ от угла сдвига – γ, то получим выражение закона Гука при кручении:

(1)

где: γ – угол закручивания, радиан

Mk – крутящий момент, Η м

I – длина образца, м

G – модуль сдвига. Па

Jp – полярный момент инерции (м4), который для полого вала равен:

(2)

где: dH – наружный диаметр

dB – внутренний диаметр сечения.

Рис.3. Напряжения и деформации при кручении

При известных значениях i и Jp можно, измерив крутящий момент Мк и соответствующий угол закручивания посчитать вели­чину модуля сдвига G , выразив его из формулы (1):

%

(3)

Угол закручивания (φ) определяется с помощью приспособления, закрепленного на теле образца (рис.4).

Приспособление для измерения угла закручивания состоит из двух рычагов 3 и 4 жестко закрепленных на образце 1 на рас­стоянии i друг от друга. На рычаге 3 укреплен индикатор часового типа 2, измерительный наконечник которого контактирует с рыча­гом 4. При закручивании образца происходит взаимное перемеще­ние (Δ) концов обоих рычагов, которое измеряется с помощью индикатора 2 (рис.5). Угол закручивания образца (Δφ= tgAcp , ввиду малости этого угла ) равен:

(4)

где: Δ – взаимное смещение концов рычагов 3 и 4, измеряемое индикатором 2;

Ки – расстояние от оси образца до измерительного наконечника индикатора, показанное на рис.5 (Ки = гн + а).

Рис.4. Образец с приспособлением для измерения угла за­кручивания

6. ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ

1. Перед испытанием студентам необходимо ознакомиться с уст­ройством машины КМ-50 (первое занятие) и правилами пове­дения в лаборатории при проведении испытаний (вводный инструктаж).

Рис.5. Схема измерения угла закручивания

2. Измеряют штангенциркулем характерные линейные размеры испытуемого образца, расстояния между обоймами приспособ­ления для измерения угла закручивания и от образующей об­разца до центра наконечника индикатора часового типа («а» на рис.5 ).

3. Приступая к испытанию необходимо дать предварительную не­большую нагрузку для устранения зазоров и обжатия образца, и провести первые отсчеты по приборам (силоизмерителю и ин­дикатору), лучше, если можно, приборы установить

4. Вручную производят статическое нагружение образца крутя­щим моментом равными ступенями ΔΜΚ . Нагружение следует производить плавно, без рывков рукоятки.

5. После каждого увеличения крутящего момента на величину ΔΜΚ снимают отсчет по индикатору (число делений индикато­ра). Запись отсчетов производят в таблицу, графы 1 и 3.

6. В процессе проведения испытаний внимательно следят за ком­ментариями преподавателя и при завершении испытаний по его указанию приступают к обработке результатов испытания.

7. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ

Обработка результатов испытания производится с помощью таблицы. На каждой ступени приращения момента ΔΜΚ определяют приращения отсчетов по индикатору ΔΑ , вычитая из показания индикатора А на каждом этапе нагружения показания его на пре­дыдущем этапе нагружения. Полученные результаты ΔΑ записыва­ют в графу 4.

Угол закручивания ( в минутах ) для каждого значения крутящего момента (графа 1 ) определяется по формуле:

Полученные значения угла закручивания заносятся в графу 5 .

Среднее приращение отсчетов АсрА определяется суммиро­ванием приращений отсчетов ΔΑ (графа 4) с последующим делени­ем на количество приращений отсчетов:

где η – количество приращений отсчетов.

Средний угол закручивания (в радианах) определяется делением среднего приращения отсчетов А на радиус R

(5)

Модуль сдвига G определяется по формуле ( 3 ) с учетом то­го что мы берем не полные углы закручивания, а средние их при­ращения, т.е.:

где: t – расчетная длина (расстояние между точками крепления обойм приспособления для измерения угла закручива­ния на испытуемом образце);

Jp – полярный момент инерции сечения образца, определя­ется по формуле (2);

Мк – среднее приращение крутящего момента; Лсрф – средний угол закручивания ( в радианах ) на базовой

длине , определяется по формуле (5).

Для проверки справедливости закона Гука при данном ис­пытании строится график в координатах (φ – Мк). По оси абсцисс откладываются углы закручивания (q>j) , а по оси ординат – соответ­ствующие им крутящие моменты (М-,- )· Полученные точки соединяют между собой отрезками прямых. В идеальном случае точки диаграммы должны лежать на одной прямой. Чем дальше от пря­мой отстоят эти точки, тем хуже материал образца подчиняется закону Гука. Существует связь между модулем упругости первого рода ( Ε), модулем упругости второго рода ( G ) и коэффициентом Пуас­сона (μ ):

Поэтому при анализе полученных результатов испытания и последующих выводах нужно воспользоваться ранее полученными значениями для Ε и μ ( лабораторная работа N 3 ), посчитать мо­дуль сдвига G и сравнить его с найденным в данном испытании.