METALS MECHANICAL PROPERTIES.
When a force or system of forces is applied to a metal sample, it reacts by changing its shape (deforming).
Various characteristics that determine the behavior and final state of a metal sample, depending on the type and intensity of forces, are called mechanical properties of the metal. Also on the topic:
PHYSICAL METAL SCIENCE
The intensity of the force acting on the sample is called stress and is measured as the total force divided by the area over which it acts. Deformation refers to the relative change in sample dimensions caused by applied stresses.
ELASTIC AND PLASTIC DEFORMATION, DESTRUCTION
If the stress applied to the metal sample is not too great, then its deformation turns out to be elastic - as soon as the stress is removed, its shape is restored. Some metal structures are deliberately designed to deform elastically. Thus, springs usually require a fairly large elastic deformation. In other cases, elastic deformation is minimized. Bridges, beams, mechanisms, devices are made as rigid as possible. The elastic deformation of a metal sample is proportional to the force or sum of forces acting on it. This is expressed by Hooke's law, according to which stress is equal to elastic strain multiplied by a constant coefficient of proportionality called the modulus of elasticity: s
=
eY
, where
s
is stress,
e
is elastic strain, and
Y
is the elastic modulus (Young’s modulus).
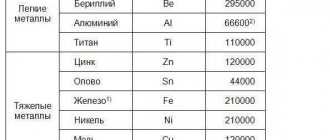
The elastic moduli of a number of metals are presented in Table. 1. Table1. Modulus of elasticity of metals
| Table 1 | ||||||
| Metal | Tungsten | Iron (steel) | Copper | Aluminum | Magnesium | Lead |
| Young's modulus, 105 MPa | 3,5 | 2,0 | 1,1 | 0,70 | 0,45 | 0,18 |
Using the data from this table, you can calculate, for example, the force required to stretch a steel rod of square cross-section with a side of 1 cm by 0.1% of its length:
Also on topic:
CORROSION OF METALS
F
=
Y
ґ
A
ґD
L
/
L
= 200,000 MPa ґ 1 cm2ґ0.001 = 20,000 N (= 20 kN)
When stresses in excess of its elastic limit are applied to a metal specimen, they cause plastic (irreversible) deformation, resulting in a permanent change in its shape. Higher stresses can cause material failure.
Also on topic:
METALS TESTING
The most important criterion when choosing a metal material that requires high elasticity is the yield strength. The best spring steels have almost the same modulus of elasticity as the cheapest construction steels, but spring steels are able to withstand much greater stresses, and therefore much greater elastic deformations without plastic deformation, because they have a higher yield strength.
The plastic properties of a metallic material (as opposed to the elastic properties) can be changed by alloying and heat treatment. Thus, the yield strength of iron can be increased 50 times using similar methods. Pure iron goes into a state of fluidity already at stresses of the order of 40 MPa, while the yield strength of steels containing 0.5% carbon and several percent of chromium and nickel, after heating to 950 ° C and hardening, can reach 2000 MPa.
When a metallic material is loaded beyond its yield strength, it continues to deform plastically, but becomes harder as it deforms, so that increasing stress is required to further increase the deformation. This phenomenon is called deformation or mechanical hardening (as well as work hardening). It can be demonstrated by twisting or repeatedly bending a metal wire. Strain hardening of metal products is often carried out in factories. Brass sheets, copper wires, and aluminum rods can be cold rolled or cold drawn to the level of hardness required for the final product.
Starlit
This is a plastic that can withstand incredibly high temperatures: its thermal threshold is so high that at first they simply did not believe the inventor. Only after demonstrating the capabilities of the material live on television, employees of the British Atomic Weapons Center contacted the creator of starlite.
Scientists irradiated the plastic with high-temperature flashes equivalent to the power of 75 bombs dropped on Hiroshima - the sample was only slightly charred. One tester noted: “Usually you have to wait several hours between flashes for the material to cool. Now we irradiated him every 10 minutes, and he remained unharmed, as if in mockery.”
Morris Ward
Unlike other heat-resistant materials, Starlite does not become toxic at high temperatures, and it is also incredibly lightweight. It can be used in the construction of spacecraft, airplanes, fireproof suits or in the military industry, but, unfortunately, starlite never left the laboratory: its creator Morris Ward died in 2011 without patenting his invention and leaving no descriptions . All that is known about the structure of starlite is that it contains 21 organic polymers, several copolymers and a small amount of ceramics.
Stretching.
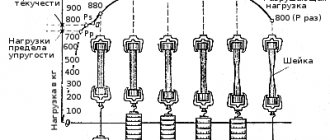
The relationship between stress and strain for materials is often examined by carrying out tensile tests, and in this case a tensile diagram is obtained - a graph in which strain is plotted along the horizontal axis and stress is plotted along the vertical axis (Fig. 1). Although tension reduces the cross-section of the specimen (and increases its length), the stress is usually calculated by relating the force to the original cross-sectional area rather than to the reduced cross-sectional area, which would give the true stress. For small deformations this does not matter much, but for large ones it can lead to a noticeable difference. In Fig. Figure 1 shows stress-strain curves for two materials with unequal ductility. (Plasticity is the ability of a material to elongate without destruction, but also without returning to its original shape after removing the load.) The initial linear section of both curves ends at the point of the yield stress, where plastic flow begins. For a less ductile material, the highest point on the diagram, its tensile strength, corresponds to failure. For a more ductile material, the ultimate tensile strength is achieved when the rate of decrease in cross-section during deformation becomes greater than the rate of strain hardening. At this stage during the test, necking begins (local accelerated reduction in cross-section). Although the specimen's ability to withstand the load decreases, the material in the neck continues to strengthen. The test ends with a cervical rupture.
Typical values of quantities characterizing the tensile strength of a number of metals and alloys are presented in table.
2. It is easy to see that these values for the same material can vary greatly depending on the processing. table 2
| table 2 | ||||
| Metals and alloys | State | Yield strength, MPa | Tensile strength, MPa | Elongation, % |
| Mild steel (0.2% C) | Hot rolled | 300 | 450 | 35 |
| Medium carbon steel (0.4% C, 0.5% Mn) | Hardened and tempered | 450 | 700 | 21 |
| High strength steel (0.4% C, 1.0% Mn, 1.5% Si, 2.0% Cr, 0.5% Mo) | Hardened and tempered | 1750 | 2300 | 11 |
| Gray cast iron | After casting | – | 175–300 | 0,4 |
| Aluminum is technically pure | Annealed | 35 | 90 | 45 |
| Aluminum is technically pure | Strain-hardened | 150 | 170 | 15 |
| Aluminum alloy (4.5% Cu, 1.5% Mg, 0.6% Mn) | Aging hardened | 360 | 500 | 13 |
| Sheet brass (70% Cu, 30% Zn) | Fully Annealed | 80 | 300 | 66 |
| Sheet brass (70% Cu, 30% Zn) | Strain-hardened | 500 | 530 | 8 |
| Tungsten, wire | Drawn to 0.63mm diameter | 2200 | 2300 | 2,5 |
| Lead | After casting | 0,006 | 12 | 30 |
ELASTIC PROPERTIES OF METALS AND ALLOYS ON THE EVE OF MARTENSITIC TRANSFORMATIONS
Published in 2021, Issue No. 2(80) February 2021, PHYSICAL AND MATHEMATICAL SCIENCES | No comments yet
ELASTIC PROPERTIES OF METALS AND ALLOYS ON THE EVE OF MARTENSITIC TRANSFORMATIONS
Research Article
Muslov S.A. *
ORCID 0000-0002-9752-6804,
Moscow State Medical and Dental University (MGMSU) named after. A.I. Evdokimov Ministry of Health of the Russian Federation, Moscow, Russia
* Corresponding author (muslov[at]mail.ru)
annotation
A review of the elastic behavior of materials in the temperature range preceding martensitic transformations (MT) is performed. It is emphasized that the nature of the change in elastic constants on the eve of these transformations is extremely informative when studying both the mechanisms and the nature of structural transitions, since elastic moduli determine the resistance of the crystal lattice to uniform shears and affect the stability of structures during martensitic rearrangement. All metals and their compounds can be divided into three groups according to the nature of the change in elastic properties. In group 1, the temperature dependence of the elastic moduli is normal (the temperature coefficient is less than zero) and phase transformations occur far from the point of loss of stability of metals and intermetallic compounds. Common to all compounds of group 2 is the anomalous “softening” of the elastic constants of alloy single crystals before MT. In this case, as a rule, the elastic constant corresponding to the Bain deformation and structural rearrangement of the lattice “softens”; it is also less than all other constants cij. Alloys of the 3rd group are characterized by an anomalous decrease in modulus and a sharp increase in elastic anisotropy A = c44/ to catastrophic values. Some intermetallic compounds are characterized by the type of pre-martensitic instability found in B2 compounds based on titanium nickelide and consisting in the simultaneous “softening” of all shear and longitudinal elastic moduli and a decrease in the coefficient of elastic anisotropy. As a result, the lattice becomes soft in all major shear systems, which provides a variety of structural phase transitions in this group of alloys and unique properties of shape memory and superelasticity.
Key words: elastic properties, martensitic transformations.
ELASTIC PROPERTIES OF METALS AND ALLOYS BEFORE MARTENSITE TRANSFORMATIONS
Research article
Muslov SA *
ORCID 0000-0002-9752-6804,
AI Yevdokimov Moscow State University of Medicine and Dentistry (MSUMD), Ministry of Health of the Russian Federation, Moscow, Russia
* Corresponding author (muslov[at]mail.ru)
Abstract
A review of the elastic behavior of materials in the temperature region before martensitic transformations (MP) is carried out. The nature of changes in elastic constants before these transformations is extremely informative in studying both the mechanisms and the nature of structural transitions, since elastic modules determine the resistance of the crystal lattice to uniform shifts and influence the stability of structures during martensitic rearrangement. All metals and their alloys by the nature of the change of elastic properties can be divided into three groups. In the 1st group, the temperature dependence of the elastic moduli is normal (the temperature coefficient is less than zero) and phase transformations take place far from the point of loss of stability of metals and intermetallic compounds. The anomalous “softening” of elastic constants of single crystals of alloys before the MP is common for all compounds of the 2nd group. In this case, as a rule, the elastic constant “softens”, corresponding to the Bane deformation and lattice structural adjustment, it is smaller than all the other constants cij. Alloys of the 3rd group are characterized by an anomalous decrease in the modulus and a sharp increase in the elastic anisotropy А = с44/ to dramatic values. The part of the intermetallic compounds is characterized by the type of premartensitic instability, found in B2 compounds based on titanium nickelide and consisting in the simultaneous “softening” of all the shear and longitudinal moduli of elasticity and a decrease in the elastic anisotropy coefficient. As a result, the lattice becomes soft in all major shear systems, which ensures the diversity of structural phase transitions in this group of alloys and the unique properties of shape memory and super elasticity.
Keywords: elastic properties, martensitic transformations.
Introduction
Martensitic transformations (MT) in metals and alloys are, as a rule, preceded by regular changes in the structure and properties of materials. Such changes are often abnormal. To date, a large amount of experimental data has been accumulated on the pre-transition behavior of physical and mechanical properties and the evolution of the crystalline and electronic structure of metals and alloys (Table 1). Despite all the diversity of observed pre-transition phenomena, their information content is unequal. Having a relatively high sensitivity, some of the physical characteristics (electrical resistance, thermal properties and others) only record the presence of pre-transition states, but are of little information in terms of elucidating the physical nature of these states and their genetic connection with subsequent MT. More direct information about the state of a material on the eve of phase transitions comes from studying its elastic properties. In this case, data on the elastic constants cij of single crystals directly reflect the nature and magnitude of interatomic bonds and the stability of the initial phases and the formation of pre-martensitic and martensitic structures. In the linear approximation, the elastic properties of cubic crystals are completely described by a matrix that contains three independent elastic constants c11, c12 and c44. Of these, the constant c44 has a direct physical meaning as a measure of the resistance of a crystal to shear in the cube plane [100] along any direction lying in this plane. Matrix elements c11 and c12 do not have such a direct interpretation. But their linear combinations B are measures of the resistance of crystals to hydrostatic compression and shear in the {110} plane in the directions. In addition, an anomalously low value may indicate the presence of a “soft” mode in the long-wavelength part of the phonon spectrum of the TA2 cubic lattice in the pre-martensitic region. At the same time, c44 and are always the largest and smallest shear moduli in a cubic crystal (less often vice versa). That is why the degree of elastic anisotropy of crystals is most often determined by the ratio. It characterizes the degree of crystal resistance to two main types of shear deformation. For an elastically isotropic crystal. The vast majority of metals and alloys are elastically anisotropic and... When metals and alloys are cooled, the elastic moduli increase, and the temperature coefficient dсij/сijdT is usually [1], i.e. –(2-5)% at 100°C.
Table 1 - Information about anomalies in the properties and structure of crystals on the eve of phase transitions
| Physical and mechanical properties, atomic-crystalline and electronic structure | Anomalous characteristics |
| Optical properties | Refractive and reflective indices, optical conductivity, real and imaginary part of complex dielectric constant, fine structure of X-ray emission and absorption spectra |
| Kinetic properties | Diffusion mobility of atoms |
| Thermal properties | Heat content, thermo emf, heat capacity, coefficient of thermal expansion |
| Magnetic properties | Hall coefficient, magnetic susceptibility, magnetoresistance |
| Electrical properties | Electrical resistivity, exoelectronic emission |
| Mechanical properties | Fragility, hardness, resistance to microplastic deformation, ductility. yield strength, martensitic shear stress |
| Acoustic properties | Acoustic emission, speed and sound attenuation |
| Elastic properties | Elastic moduli of polycrystals, elastic constants of the 2nd and 3rd order of single crystals |
| Phononic subsystem | Phonon spectrum, effects of diffuse scattering of electrons, X-rays and neutrons, NGR parameters |
| Electronic subsystem | Density of states function, Fermi surface topology, charge density waves (CDWs) |
Depending on the behavior of cij in the temperature range preceding the MT, three groups of metals and alloys can be distinguished [2] (Table 2).
Table 2 – Pre-martensitic behavior of elastic properties in materials
| Group A Materials with a stable lattice | Group B Materials with a tendency to decrease stability | Group B Materials with a sharp decrease in stability |
| Fe-C, Fe-Cr-Ni, Fe-Mn-C, Co, Co-Ni, Fe-Ni, (< 30 at.% Ni), Li (b.c.c.-g.p.s., MS=78 K), Na (b.c.c.-g.p.s., MS=35 K) | Hume-Rothery β-phases: CuZnAl, CuAlNi, CuZn, CuSn, Cu3-xMnxAl, AuZn, Au-Cd, AuAgCd, AuCuZn, AgZn, AgCd, NiAl, Ti, Zr, Hf, Ti (Mo, V, Nb), Ti-Cr, Zr-Nb. TiNi. Fe-Ni (> 30 at.% Ni), Fe-Pt (near Fe3Pt), Fe-Pd, U | Superconducting compounds: A15 (V3Si, Nb3Sn), A1 (In-Tl, In-Cd,) C15 (V2Zr, V2Hf), antiferromagnetic alloys: A1 (Mn-Cu, Ni-Mn, AuMn-AuZn) |
Group A
This group consists mainly of alloys based on α-iron, as well as alkali metals Li and Na [3, 4]. MTs in them are clearly expressed phase transitions of the 1st order with a normal temperature dependence of elastic properties dcij/dT < 0 (Fig. 1, a). In the pre-transition temperature region, only certain characteristics of materials experience weak anomalies. Thus, MTs in this group of metals and alloys occur far from the point of loss of mechanical stability of the crystal lattice.
Group B
It is formed by numerous Hume-Rothery β-phases based on copper, silver and gold with an ordered bcc structure B2 (CsCl) and DO3 (Fe3Al type) and a fcc superstructure of the Heusler type L12 (Cu2MnAl), B2 transition metal alloys with components to the right and left of the group chromium NiAl, TiNi, group IY metals [Ti, Zr, Hf] and solid solutions based on them (crystalline type A2), as well as ferromagnetic Fe-Ni, Fe-Pt and Fe-Pd fcc disordered A1 and superlattice-ordered L12 alloys . Common to all compounds is the “softening” of the elastic constants of alloy single crystals before MT. “Softening” usually means a deviation from the linear dependence of the temperature dependence of the elastic constants or their combinations. In this case, as a rule, the elastic constant corresponding to the Bain strain [5] “softens”; it is also less than all other constants cij (Fig. 1, b).
Rice. 1 – Elastic constants cij near the MP: (a) Na, (b) CuZnAl, AuCd, (c) FePt, InTl, InCd, (d) V3Si, Nb3Sn, (e) ZrNb, (f) FeNi
Rice. 2 – The magnitude of elastic constants с44, and the coefficient of elastic anisotropy of single crystals of various alloys near MT temperatures
In some alloys with a β-phase structure, Nagasawa et al. also discovered “soft” modes, but slightly different behavior of elastic constants [6]. In addition to the constant , which “softens” long before the transition, starting from a certain temperature, there is a “softening” of the “special mode” cS, which controls the shear system close to {112}<111>. As is known, the authors emphasize, this shift corresponds to the second stage of the restructuring of the o.c.c. structures upon transition to g.p.u. phase according to the Burgers scheme.
In Zr-Nb alloys, elastic anomalies precede the formation of the ω-phase, which is widespread in unstable titanium and zirconium alloys [7]. The elastic constant c44 experiences a slight “softening” before MS at normal temperature dependence of the coefficients and c11. At the same time, elastic anisotropy A is small, and on the eve of the transition it further decreases (Fig. 1, e). It has also been established that when ZrNb is doped with Nb atoms together with Zr and the A2 structure is stabilized towards the transition, the elastic moduli become “harder” and the elastic anomalies degenerate.
In iron-nickel alloys [8], “softening” of the elastic moduli occurs only when the Curie point Tc is located above Ms, which occurs when the nickel content in the alloys is more than 30% (Fig. 1, f). In these alloys, elastic anomalies are caused by the formation of a magnetic structure. In single crystals of a disordered Fe-Pt alloy with an A1 structure, near the stoichiometric composition (platinum concentration according to chemical analysis is 28.15 at.%) due to the Invar properties of the alloy before f.c.c.-b.c.c. transition, all elastic constants сL = 1/2 (c11+c12 +2c44), and с44 have anomalies (Fig. 1, c).
Group B
It includes compounds of the crystalline type A15 with a β-tungsten type structure (V3Si, Nb3Sn), A1 (InTl, InCd, ...) and C15 (V2Zr, V2Hf), which, on the eve of the transition to the superconducting state, undergo structural phase transitions of the martensitic type, and also antiferromagnetic A1 alloys based on γ-Mn, which experience antiferromagnetic ordering at the Néel point, accompanied by magnetostrictive distortion of the original cubic lattice. In these alloys, MTs are close to second-order phase transitions and are preceded by intense “softening” of the elastic lattice constants, sometimes several at the same time (Fig. 1, c, d). When studying the elastic constants in V3Si single crystals in the temperature range 4.2-300 K, it was found that the value of the constants c11 and c44 upon cooling decreases by 37.4% and 5.8%, respectively. The shear modulus undergoes an even greater change: cooling V3Si from 300 to 25 K leads to a 10-fold decrease. At the same time, c44 weakly depends on temperature. A similar behavior of the elastic moduli of single crystals was recorded in the isostructural compound Nb3Sn. An anomalous decrease in modulus and an increase in elastic anisotropy A = c44/ to catastrophic values (Fig. 2) were also observed in InTl and InCd alloys with a shape memory effect on the eve of the fcc-hc transition. Finally, critically strong “softening” was discovered in γ-manganese alloys before the formation of tetragonal martensite, as well as in binary intermetallic superconducting Laves type A2B phases V2Zr and V2Hf at the cubic-rhombohedral and cubic-tetragonal lattice transitions, respectively.
TiNi based alloys
Until some time ago, there were isolated cases [9] of measuring elastic constants in single crystals of TiNi, an intermetallic compound known for the most pronounced shape memory and superelasticity effects among alloys [10]. As a rule, this was explained by the technical difficulties that arose when trying to grow crystals of this alloy with dimensions that would be suitable for ultrasound research. It is interesting to note that both constants of c44 and NiTi crystals had relatively low values and decreased further upon cooling. In the range 293-303K, that is, the rate of decline of c44 is more than twice as high as that of (+11.4 and +28.3% per 100 K). As a result, the anisotropy coefficient of the alloy varies from 2.18 at 313 K to 1.90 at 278 K and is not anomalously large as in other alloys that experience MT and have shape memory (Fig. 2). The elastic constants of NiTi-based single crystals were studied in great detail in [11], [12].
In [13], a comparison was made of the elastic behavior of alloys based on titanium nickelide and other intermetallic compounds with a bcc lattice in the temperature range preceding martensitic transitions in them (Table 3).
Table 3 - Comparison of the elastic properties of TiNi with the elastic properties of other bcc alloys near the MP
Note: *Here “softening” means partial softening, SBP – shift in the basal plane ().
In [14], the elastic constants of single crystals of TiNi-TiFe alloys were studied, stable and gradually losing stability, first to one B2-R, and then to two B2-R-B19′ MPs (Fig. 3). This made it possible to relate the evolution of elastic properties to changes in the structure of the alloys.
Rice. 3 – Behavior of elastic lattice constants c44 (a) and (b) Ti50Ni50-хFeх single crystals, x=50, 25, 10, 5, 2 (1-5) and Ti49Ni51 (6), respectively
In alloys based on TiFe (Ti50Fe50 and Ti50Ni25Fe25), the composition of which is far from alloys with MT, the elastic lattice constants C' and c44 behave normally during cooling (dC'/dT < 0, dc44/dT < 0), and their values are sufficient high. Only the following features of the elastic characteristics of the alloys can be noted: the anisotropy of Ti50Fe50 () crystals, rare for metal systems, and, as a result of the decrease in modulus C', the almost complete isotropy of the elastic properties of the Ti50Ni25Fe25 () intermetallic lattice. The first obvious signs of a decrease in the stability of the B2 structure of the alloys under study are observed in alloys with a transitional iron content (at.%). In Ti50Ni35Fe15, the normal temperature dependence of C'(T) and c44(T) gradually becomes anomalous below a certain temperature. Since, with increasing nickel content, C' decreases more intensely than c44, the elastic anisotropy coefficient in this alloy becomes greater than unity. In Ti50Ni40Fe10, “softening” of the elastic constants is observed throughout the entire temperature range studied (77-873 K) and intensifies in the low temperature region. However, this “softening” does not reach critical values and MPs are not realized. Thus, anomalous behavior of elastic moduli in the pre-martensitic range of states can be observed even in materials that do not experience MTs themselves. Finally, in TiNi-based alloys, pronounced anomalies in elastic properties end with the transformation of B2-R into Ti50Ni45Fe5 (at 185 K) and chains of transformations B2-R-B19′ into Ti50Ni48Fe2 and Ti49Ni51 at temperatures below 240 and 285 K, respectively. Near structural transitions, the “softening” of the alloy lattice increases, and c44 experiences stronger changes than C'. As a result, the initial B2 lattice approaches elastically isotropic, and its resistance to deformation becomes abnormally low in all main crystallographic shear systems (Table 4).
Table 4 – Elastic moduli in the main crystallographic systems of atomic displacements in cubic crystals
The low value of A indicates that the studied alloys contain several “soft” shear systems, etc., which provides a variety of structural phase transformations and their chains in this group of alloys and unique properties of shape memory and superelasticity. The same thing—the presence of “soft” modes—is evidenced by strands in certain directions of the reciprocal lattice and extrareflections in certain positions in microdiffraction patterns in TiNi-based alloys [15, 16].
| Acknowledgments The work was carried out in accordance with the research plan AAAA-A16-116102010059-6 FGANU CITiS (2017-2021) of the Department of Science and Mathematics of the Moscow State Medical University named after. A.I. Evdokimov. | Acknowledgment The work was carried out in accordance with the research plan AAAA-A16-116102010059-6 of FSANU CITIS (2017–2021) of the Department of NF and MF AI Evdokimova MSUMD. |
| Conflict of interest Not specified. | Conflict of Interest None declared. |
List of literature / References
- Elastic constants and moduli of elasticity of metals and nonmetals: Handbook. Ed. I.N. Frantsevich. Kyiv: Naukova Dumka (1982) 286 p.
- Guénin G. Contribution a l'etude de la nucleation transformations martensitiques thermoelastiques cas de l'alliage ternaire Cu-Zn-Al /G. Guénin // These... docteur-ingenieur. Lyon, 1979. 167 rub.
- Everson JH Phys. Status solidi / JH Everson, JH Chen, Ph. C. Clapp // A59 2 795 (1980).
- Martinson RH Phys. Rev/RH Martinson. 178 3 902 (1969).
- Landa M. Materials Science and Engineering / M. Landa A 462 320 (2007).
- Nagasawa A. Proc. Int Conf. Martensitic Transform / A. Nagasawa // ICOMAT (1979) Cambridge, Mass., USA. 423 (1979).
- Goasdoue C. Acta met / C. Goasdoue, PS Ho, SL Sass // 20 5 725 (1972).
- Robin M. Etude de la transformation martensitique en avalanche d᾿un alliage de fer a 32% de nickel et de l᾿emission electrique associee. Thèse… docteur d᾿etat es-siences / M. Robin. Lyon, (1981) 249 p.
- Mercier O. Appl. Phys / O. Mercier, KN Melton, G. Gremaud, JJ Hagi. (1980) 51 3 1833.
- Muslov S. A. Application of materials with shape memory effect in science, technology and medicine CA Muslov. – M.: Publishing house “Folium” (2007) 328 p.
- Kuznetsov A.V. News of universities, ser. Physics / AB Kuznetsov, CA Muslov, A. I. Lotkov. (1987) 7 98.
- Muslov S. A. News of universities, ser. Physics / S. A. Muslov, A. V. Kuznetsov, V. N. Khachin et al. (1987) 8
- Otsuka K. Progress in Materials Science / Otsuka H. Ren. 50,511 (2005).
- Muslov S.A. Pre-martensitic states in single crystals of TiNi-TiFe and TiNi-TiCu alloys: (01.04.07): Dis. for the job application scientist step. Ph.D. physics and mathematics Sciences / Vol. state University named after V.V. Kuibysheva / CA Muslov, 1987. – 166 p.
- Khachin V. N. Reports of the USSR Academy of Sciences / V. N. Khachin, C. A. Muslov, V. G. Pushin et al. (1987) 295 3 606.
- Muslov S. A. Letters on materials / S. A. Muslov, V. N. Khachin, V. G. Pushin et al. (2015) 5 4 420.
List of literature in English / References in English
- Uprugiye postoyannyye i moduli upru-gosti metallov i nemetallov Ed. by IN Frantsevich. Kiev: Naukova Dumka (1982) 286 p.
- Guénin G. Contribution a l'etude de la nucleation transformations martensitiques thermoelastiques cas de l'alliage ternaire Cu-Zn-Al /G. Guénin // These... docteur-ingenieur. Lyon, 1979. 167 RUR
- Everson JH Phys. Status solidi / JH Everson, JH Chen, Ph. C. Clapp // A59 2 795 (1980).
- Martinson RH Phys. Rev/RH Martinson. 178 3 902 (1969)
- Landa M. Materials Science and Engineering / M. Landa A 462 320 (2007).
- Nagasawa A. Proc. Int Conf. Martensitic Transform / A. Nagasawa // ICOMAT (1979) Cambridge, Mass., USA. 423 (1979).
- Goasdoue C. Acta met / C. Goasdoue, PS Ho, SL Sass // 20 5 725 (1972).
- Robin M. Etude de la transformation martensitique en avalanche d᾿un alliage de fer a 32% de nickel et de l᾿emission electrique associee. Thèse… docteur d᾿etat es-siences / M. Robin. Lyon, (1981) 249 p.
- Mercier O. Appl. Phys / O. Mercier, KN Melton, G. Gremaud, JJ Hagi. (1980) 51 3 1833.
- Muslov SA Primeneniye materialov s effektom pamya-ti formy v nauke, tekhnike i medicitsine / SA Muslov. – M.: Publishing house “Folium” (2007) 328 p.
- Kuznetsov AV Izvestiya vuzov, ser. Fizika / AV Kuznetsov, A. Muslov, AI Lotkov and others (1987) 7 98.
- Muslov S. Izvestiya vuzov, ser. Fizika / SA Muslov, AV Kuznetsov, VN Khachin and others. (1987) 8.104.
- Otsuka K. Progress in Materials Science 50 511 / K. Otsuka, X. Ren. (2005).
- Muslov SA Predmartensitnyye so-stoyaniya v monokristallakh splavov TiNi-TiFe i TiNi-TiCu: / SA Muslov (01.04.07): PhD thesis in Physics and Mathematics / Tomsk state university named after VV Kuibyshev, 1987. – 166 p. [In Russian]
- Khachin VN Doklady AN SSSR / VN Khachin, SA Muslov, VG Pushin and others. Academy of Sciences (1987) 295 3 606.
- Muslov S. Pis'ma o materialakh (2015) / SA Muslov, VN Khachin, VG Pushin and others. 5 4 420.
Compression.
Elastic and plastic properties under compression are usually very similar to those observed under tension (Fig. 2). The curve of the relationship between conditional stress and conditional strain in compression passes above the corresponding curve for tension only because during compression the cross-section of the sample does not decrease, but increases. If we plot true stress and true strain along the axes of the graph, then the curves practically coincide, although failure occurs earlier in tension.
Hardness.
The hardness of a material is its ability to resist plastic deformation. Since tensile tests require expensive equipment and a lot of time, simpler hardness tests are often used. When testing using the Brinell and Rockwell methods, an “indenter” (a tip shaped like a ball or pyramid) is pressed into the metal surface at a given load and loading speed. Then the size of the print is measured (often done automatically) and the hardness index (number) is determined from it. The smaller the imprint, the greater the hardness. Hardness and yield strength are to some extent comparable characteristics: usually, as one increases, the other also increases.
It may seem that in metallic materials maximum yield strength and hardness are always desirable. In fact, this is not the case, and not only for economic reasons (hardening processes require additional costs).
First, materials need to be shaped into various products, and this is usually done using processes (rolling, stamping, pressing) in which plastic deformation plays an important role. Even when processed on a metal-cutting machine, plastic deformation is very significant. If the hardness of the material is too high, then too much force is required to give it the desired shape, as a result of which the cutting tools quickly wear out. This kind of difficulty can be reduced by processing metals at elevated temperatures, when they become softer. If hot processing is not possible, then metal annealing (slow heating and cooling) is used.
Second, as a metal material gets harder, it usually loses its ductility. In other words, a material becomes brittle if its yield strength is so high that plastic deformation does not occur up to those stresses that immediately cause failure. The designer usually has to choose some intermediate levels of hardness and ductility.
Airgel
Imagine a porous substance of such low density that 2.5 cm³ of it contains surfaces comparable to the size of a football field. But it's not a specific material, but rather a class of substances: airgel is a form that some materials can take, and its ultra-low density makes it an excellent thermal insulator. If you make a 2.5 cm thick window out of it, it will have the same thermal insulation properties as a 25 cm thick glass window.
All the lightest materials in the world are aerogels: for example, quartz aerogel (essentially dried silicone) is only three times heavier than air and is quite fragile, but can withstand a weight 1000 times its own. Graphene airgel (illustrated above) consists of carbon, and its solid component is seven times lighter than air: having a porous structure, this substance repels water, but absorbs oil - it is supposed to be used to combat oil spills on the surface of water.
Impact strength and brittleness.
Toughness is the opposite of brittleness. This is the ability of a material to resist destruction by absorbing impact energy. For example, glass is brittle because it cannot absorb energy through plastic deformation. With an equally sharp blow on a sheet of soft aluminum, large stresses do not arise, since aluminum is capable of plastic deformation, which absorbs the impact energy.
There are many different methods for testing metals for impact strength. When using the Charpy method, a prismatic sample of metal with a notch is subjected to the impact of a retracted pendulum. The work expended on the destruction of the sample is determined by the distance by which the pendulum deviates after the impact. Such tests show that steels and many metals behave as brittle at low temperatures, but as ductile at elevated temperatures. The transition from brittle to ductile behavior often occurs over a fairly narrow temperature range, the midpoint of which is called the brittle-ductile transition temperature. Other impact tests also indicate the presence of such a transition, but the measured transition temperature varies from test to test depending on the depth of the notch, the size and shape of the specimen, and the method and speed of impact loading. Since no single type of test reproduces the full range of operating conditions, impact tests are only valuable in that they allow comparisons between different materials. However, they provided much important information about the effects of alloying, fabrication techniques, and heat treatment on the susceptibility to brittle failure. The transition temperature for steels, measured using the Charpy V-notch method, can reach +90°C, but with appropriate alloying additives and heat treatment it can be lowered to -130°C.
The brittle fracture of steel has been the cause of numerous accidents, such as unexpected pipeline breaks, explosions of pressure vessels and storage tanks, and bridge collapses. Among the most famous examples are a large number of Liberty-class seagoing vessels whose hulls unexpectedly came apart during voyage. As the investigation showed, the failure of the Liberty ships was due, in particular, to incorrect welding technology that left internal stresses, poor control over the composition of the weld and design defects. Information obtained from laboratory tests has significantly reduced the likelihood of such accidents. The brittle-ductile transition temperature of some materials, such as tungsten, silicon and chromium, under normal conditions is much higher than room temperature. Such materials are usually considered brittle, and they can be given the desired shape through plastic deformation only by heating. At the same time, copper, aluminum, lead, nickel, some grades of stainless steel and other metals and alloys do not become brittle at all when the temperature drops. Although much is already known about brittle fracture, this phenomenon is not yet fully understood.
Message 2
At the moment, humanity knows a huge number of metals, most of which have certain properties, thanks to which they can be divided into groups, subgroups, and various sets. Many of these metals are quite rare, which are found very rarely in single copies, while others, on the contrary, are so common that they are sometimes not even used. One way or another, any metal, rare or not, is worthy of attention and careful study, since it is possible that many of the properties of these metals remain undiscovered to this day.
The properties of metals are divided into chemical and physical, which are radically different from each other.
Typically, the physical properties of most metals are similar. Any metal, in the standard view of any person, is a shiny, hard, heavy, or not very, and strong material. Metals also conduct heat and electric current well, which makes them very good conductors of electricity, however, as the temperature of the metal increases, its electrical conductivity decreases, which is why metals with high heat resistance are valued.
A very important metallic physical property of a metal is its easy deformability, which allows human thought to do with this substance everything that it is capable of. Metal can be forged, flattened, cut, melted into another shape, and many other interesting things.
Chemical properties of metals.
The fundamental chemical property of metals is their ability to easily give up their valence electrons and transform into positively charged ions. Metals usually never take up electrons because their ions are always positively charged.
Easily parting with their electrons, metals can rightly be called excellent reducing agents, according to the laws of chemistry.
However, even despite all of the above, the ability to bestow does not manifest itself to the same extent. If one metal can easily give up its electrons, then the other, on the contrary, part with them very reluctantly, which creates a pattern in their reduction functions.
Based on all of the above, we can conclude that metals have a number of amazing properties, both physical and chemical, which makes their study very exciting and interesting.
Fatigue.
Fatigue is the failure of a structure under the influence of cyclic loads. When a part is bent in one direction or the other, its surfaces are alternately subjected to compression and tension. With a sufficiently large number of loading cycles, fracture can be caused by stresses that are significantly lower than those at which failure occurs in the case of a single loading. Alternating stresses cause localized plastic deformation and strain hardening of the material, as a result of which small cracks appear over time. The concentration of stress near the ends of such cracks causes them to grow. At first, the cracks grow slowly, but as the cross-section bearing the load decreases, the stresses at the ends of the cracks increase. In this case, the cracks grow faster and faster and, finally, instantly spread to the entire cross-section of the part. see also
DESTRUCTION MECHANISMS.
Fatigue is undoubtedly the most common cause of structural failure under operating conditions. Machine parts operating under cyclic loading conditions are especially susceptible to this. In the aircraft industry, fatigue turns out to be a very important problem due to vibration. Airplane and helicopter parts must be inspected and replaced frequently to avoid fatigue failure.
One way bulletproof glass
The richest people have a problem: judging by the growing sales of this material, they need bulletproof glass that will save lives, but will not stop them from shooting back.
This glass stops bullets on one side, but at the same time lets them through on the other - this unusual effect consists of a “sandwich” of a fragile acrylic layer and a softer elastic polycarbonate: under pressure, acrylic manifests itself as a very hard substance, and when a bullet hits it extinguishes its energy, cracking at the same time. This allows the shock-absorbing layer to withstand the impact of bullets and acrylic fragments without collapsing.
When fired from the other side, the elastic polycarbonate allows the bullet to pass through itself, stretching and destroying the brittle acrylic layer, which leaves no further barrier for the bullet, but you should not shoot too often, as this will create holes in the protection.
Creep.
Creep (or creep) is the slow increase in plastic deformation of a metal under the influence of a constant load. With the advent of jet engines, gas turbines and rockets, the properties of materials at elevated temperatures have become increasingly important. In many areas of technology, further development is hampered by limitations associated with high-temperature mechanical properties of materials.
At normal temperatures, plastic deformation is established almost instantly as soon as the appropriate stress is applied, and subsequently increases little. At elevated temperatures, metals not only become softer, but also deform so that the deformation continues to increase over time. This time-dependent deformation, or creep, can limit the life of structures that must operate at elevated temperatures for long periods of time.
The greater the stress and the higher the temperature, the greater the creep rate. Typical creep curves are shown in Fig. 3. After the initial stage of rapid (unsteady) creep, this speed decreases and becomes almost constant. Before failure, the creep rate increases again. The temperature at which creep becomes critical is different for different metals. A concern of telephone companies is creep in lead-sheathed overhead cables operating at normal ambient temperatures; at the same time, some special alloys can operate at 800 ° C without exhibiting excessive creep.
The service life of parts under creep conditions can be determined by either the maximum permissible deformation or fracture, and the designer must always keep these two options in mind. The suitability of materials for the manufacture of products designed for long-term operation at elevated temperatures, such as turbine blades, is difficult to assess in advance. Testing for a duration equal to the expected service life is often impractical, and the results of short-term (accelerated) tests are not easily extrapolated to longer periods, since the failure pattern may change. Although the mechanical properties of superalloys are constantly being improved, metal physicists and materials scientists will always be challenged to create materials that can withstand even higher temperatures. see also
METAL SCIENCE PHYSICAL.
CRYSTAL STRUCTURE
Above we discussed the general patterns of behavior of metals under the influence of mechanical loads. To better understand the corresponding phenomena, it is necessary to consider the atomic structure of metals. All solid metals are crystalline substances. They consist of crystals, or grains, the arrangement of atoms in which corresponds to a regular three-dimensional lattice. The crystalline structure of a metal can be thought of as consisting of atomic planes, or layers. When shear stress (a force that causes two adjacent planes of a metal specimen to slide against each other in opposite directions) is applied, a single layer of atoms can move an entire interatomic distance. Such a shift will affect the shape of the surface, but not the crystal structure. If one layer moves many interatomic distances, a “step” is formed on the surface. Although individual atoms are too small to be seen under a microscope, the steps formed by sliding are clearly visible under the microscope and are called slip lines.
Common metal objects that we encounter every day are polycrystalline, i.e. consist of a large number of crystals, each of which has its own orientation of atomic planes. The deformation of an ordinary polycrystalline metal has in common with the deformation of a single crystal that it occurs due to sliding along atomic planes in each crystal. Noticeable sliding of entire crystals along their boundaries is observed only under conditions of creep at elevated temperatures. The average size of one crystal, or grain, can range from several thousandths to several tenths of a centimeter. A finer grain size is desirable because the mechanical properties of a fine-grained metal are better than those of a coarse-grained metal. In addition, fine-grained metals are less brittle.
Shapeless metal
This substance allows golfers to hit the ball harder, increases the bullet's striking power and extends the life of scalpels and engine parts.
Contrary to its name, the material combines the strength of metal and the hardness of a glass surface: the video shows how the deformation of steel and shapeless metal differs when a metal ball falls. The ball leaves many small “pits” on the surface of the steel - this means that the metal absorbs and dissipates the impact energy. The shapeless metal remained smooth, which means it better returns the impact energy, which is also evidenced by a longer rebound.
Most metals have an ordered crystalline molecular structure, and from a blow or other impact, the crystal lattice is distorted, which is why dents remain on the metal. In a shapeless metal, the atoms are arranged randomly, so after exposure the atoms return to their original position.
Slip and dislocations.
Sliding processes were studied in more detail on single crystals of metals grown in the laboratory. It turned out not only that sliding occurs in certain specific directions and usually along very specific planes, but also that single crystals are deformed at very low stresses. The transition of single crystals to the fluid state begins for aluminum at 1, and for iron at 15–25 MPa. Theoretically, this transition in both cases should occur at voltages of approx. 10,000 MPa. This discrepancy between experimental data and theoretical calculations has remained an important problem for many years. In 1934, Taylor, Polanyi and Orowan proposed an explanation based on the idea of defects in the crystal structure. They suggested that during sliding, a displacement first occurs at some point in the atomic plane, which then propagates throughout the crystal. The boundary between the shifted and non-shifted regions (Fig. 4) is a linear defect in the crystal structure, called a dislocation (in the figure, this line extends into the crystal perpendicular to the plane of the figure). When a shear stress is applied to a crystal, the dislocation moves, causing it to slide along the plane in which it is located. Once dislocations have formed, they move very easily throughout the crystal, which explains the “softness” of single crystals.
Metal crystals usually contain many dislocations (the total length of dislocations in one cubic centimeter of annealed metal crystal can be more than 10 km). But in 1952, scientists at the Bell Telephone Corporation laboratories, testing the bending of very thin whisker crystals (whiskers) of tin, discovered, to their surprise, that the bending strength of such crystals was close to the theoretical value for perfect crystals. Later, extremely strong whiskers of many other metals were discovered. It is believed that such high strength is due to the fact that in such crystals there are either no dislocations at all, or there is one running along the entire length of the crystal.