Длина пружины растяжения формула

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

сдвиг;
кручение;
изгиб;
сжатие/растяжение;

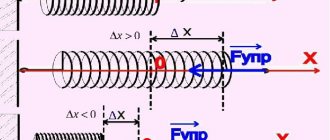
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Определение коэффициента жесткости растяжения

Для определения коэффициента жесткости растяжения производятся следующие расчеты.

Измеряется длина пружины в вертикальном подвесе с одной свободной стороной изделия – L1;
Измеряется длина пружины с подвешенным грузом – L2.Если взять груз массой 100гр., то он будет воздействовать силой в 1Н (Ньютон) – величина F;
Вычисляется разница между последним и первым показателем длины – L;
Рассчитывается коэффициент упругости по формуле: k = F/L.

Определение коэффициента жесткости сжатия производится по этой же формуле. Только вместо подвешивания груз устанавливается на верхнюю часть вертикально установленной пружины.

Подводя итог, делаем вывод, что показатель жесткости пружины является одной из существенных характеристик изделия, которая указывает на качество исходного материала и определяет долговечность использования конечного изделия.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

Как рассчитать жесткость пружины

Для расчета коэффициента жесткости применяется формула:

k = G * (Dw)^4 / 8 * Na * (Dm)^3,

где G – модуль сдвига. Данную величину можно не рассчитывать, так как она приведена в таблицах к различным материалам. Например, для обыкновенной стали она равна 80 ГПа, для пружинной – 78,5 ГПа. Из формулы понятно, что наибольшее влияние на коэффициент жесткости пружины оказывают оставшиеся три величины: диаметр и число витков, а также диаметр самой пружины. Для достижения необходимых показателей жесткости изменению подлежат именно эти характеристики.

Читать также: Медно фосфорный припой для пайки меди

Вычислить коэффициент жесткости экспериментальным путем можно при помощи простейших инструментов: самой пружины, линейки и груза, который будет воздействовать на опытный образец.

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

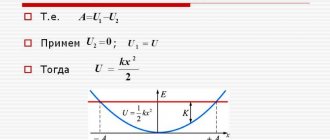
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.

Конические винтовые пружины сжатия

В тех случаях, когда требуется значительно уменьшить габаритные размеры пружины в сжатом состоянии, применяют данный вид пружин.

Высота этих пружин в сжатом состоянии равна толщине одного витка. Коническую пружину навивают таким образом, чтобы при сжатии она представляла собой спираль Архимеда с шагом «а», несколько превышающим толщину проволоки

Максимальные напряжения возникают в витке с наибольшим радиусом.

Перемещение пружины находят по формуле:

При расчете подвижных узлов механизма, которые перемещаются за счет аккумулированной энергии пружин, возникает необходимость в определении параметров этой пружины, обеспечивающих заданное время срабатывания или требуемую скорость узла.

Максимальные напряжения возникают в витке с наибольшим радиусом.

Перемещение пружины λ находят по формуле:

Время срабатывания:

где: — приведенная масса и все силы действующие на этот узел (к концу пружины

в сжатом состоянии).

Если сила Р смещена относительно оси, то это приводит к нежелательным условиям работы. Пружины сжатия теряют устойчивость, а пружины растяжения изгибаются под действием дополнительного момента. Соосности действующей силы Р и пружины достигаются применением различных способов закрепления концов пружины.

Винтовые пружины кручения

Применяют для эластичного соединения в муфтах, замыкания кинематических цепей различных механизмов, в качестве фиксаторов положения и аккумуляторов энергии. Для обеспечения продольной устойчивости пружин во время работы монтируют на направляющем стенде. При этом один конец пружины закрепляют на неподвижной стойке, а другой нагружают силой Р.

Под действием момента PI = М пружина скручивается. При этом в сечениях витков возникают нормальные напряжения от изгибающего момента Ми — М cosa и касательные от момента кручения Ми= М sina, где a — это угол подъема винтовой линии пружины. Влияние на прочность пружины касательных напряжений может быть учтено введением поправочного коэффициента К, который в зависимости от индекса пружины (С = 4 — 5) обычно равен 1,2 — 1,1. В этом случае расчет пружины проводиться только на изгиб.

Диаметр проволоки:

Средний диаметр пружины в свободном состоянии: Do — cd;

Угол закручивания пружины:

где L — длина проволоки для рабочего состояния пружины. L= Пcdn0 (n0 — число витков в свободном состоянии).

И соответственно:

При выборе направляющего стержня Dct необходимо учитывать изменение среднего диаметра пружины и число рабочих витков в процессе ее деформации. Приняв длину проволоки неизменной

Спиральные пружины

Применяют эти пружины, как в самопишущих приборах, так и в часовых и других механизмах. Спиральная пружина создает момент, действующий в плоскости перпендикулярной ее оси.

В зависимости от назначения спиральные пружины называются моментными или заводными.

Моментные применяют в приборах для создания противодействующего момента подвижной системы, в рычажных, зубчатых и других измерительных системах — для силового замыкания кинематических цепей. Эти пружины часто называют волосками. Они имеют малую площадь сечения и развивают незначительный момент. Моментные пружины -это детали приборов, от которых зависит точность измерительных систем. Так как они часто работают в специфических условиях, к ним предъявляются следующие требования:

· Зависимость момента от угла закручивания должна быть линейной.

Линия OA — зависимость М от п без учета гистерезиса (внутреннего трения). Его петля показана штриховыми линиями.

· Несовершенства свойств упругости (гистерезис и упругое быстродействие) должны быть меньше погрешности, значение которой определяется классом точности прибора.

· Температурный коэффициент модуля упругости должен быть малым.

· Материал пружины должен иметь высокую коррозионную стойкость.

· В электроизмерительных приборах материал моментных пружин должен обладать антимагнитностью и малым удельным сопротивлением.

Противодействующий момент спиральной пружины определяется значением действующего момента в электроизмерительной системе.

При использовании ее для силового замыкания кинематической цепи прибора при малых инерционных нагрузках, ее минимальный момент при предварительном угле закручивания находят в зависимости от момента трения, приведенного к ее оси.

где К — это коэффициент запаса К = 2 ÷ 3.

Приведенный момент трения, равный сумме моментов трения в определенных узлах механизма, приведенных к оси пружины.

Теоретические значения наибольшего и наименьшего моментов определяютя по формулам:

1 — длина упругой части волоска.

Определив значение необходимого момента спиральной пружины по по формуле

можно найти ее геометрические параметры из уравнений прочности и жесткости: где:

L — длина волоска.

Длина моментной спиральной пружины может быть приблизительно найдена из уравнения равенства площадей:

Таким образом, условием нормальной работы волоска будет:

Для учета различных нагрузок, возникающих в процессе работы прибора (вибрации, температура…) вводится коэффициент запаса волоска nв= 2÷3,тогда:

Приведенный момент трения в общем виде: (уравнение *).

Где:

— сумма приведенных к оси волоска моментов трения, эквивалентная моментам трения, действующим на каждую из n осей механизма. MTpj — момент на одной из n осей, ddi — угол поворота n-й оси, соответствующий повороту оси волоска на угол dω.

— сумма приведенных к оси волоска моментов трения, эквивалент моментами трения, вызванными силами трения Fipj на линейных перемещениях dsj в каждой из m поступательных парах механизма.

Число витков и шаг спирали определим по формулам:

Для обеспечения линейной характеристики необходимо крепление наружного и внутреннего концов спиральной пружины выполнить так, чтобы во время деформации ее витки оставались концентричными. На рисунке показаны способы крепления заводных пружин, которые служат для аккумулирования механической энергии в пружинных двигателях.

Пружинные двигатели бывают двух типов: с подвижным доводным барабаном и с неподвижным. Чаще применяются двигатели с подвижным барабаном.

Как мы уже говорили, моментные пружины часто используются в передаточных механизмах для устранения зазоров и т.п. При работе измерительного прибора вследствие прогиба указателя при ударах об упор и остаточной деформации пружины, стрелка может не вернуться в исходное положение. Для установки стрелки в исходное положение (нулевую отметку), ставят корректор.

В ряде случаев начальный участок шкалы измерительного прибора должен соответствовать высокой чувствительности, а конечный — более низкой. Для этой цели применяют пружину с переменной жесткостью.

В средней части пружины ставят ограничитель (1), а в неподвижной части прибора -упор (2). При повороте валика на некоторый угол , соответствующий контактному ограничителю с упором, работает вся пружина. Чувствительность получается высокой. При этом характеристика изобразится пологой прямой АС. При дальнейшем повороте

валика на больший угол, будет работать не вся пружина, а лишь ее часть от валика до упора. Жесткость пружины увеличивается, чувствительность понижается, а характеристика становиться более крутой — отрезок CD.

В качестве материала для изготовления моментных пружин применяют ленты из сталей , бронза

При расчете волосков коэффициент запаса прочности . Большое значение

коэффициента берут для получения небольших остаточных деформаций и обеспечения постоянства упругих свойств волоска.

Минимальный момент волоска , который создают путем закрутки волоска при установке в приборе, должен быть больше всех моментов трения, возникающих в подвижных соединениях передаточного механизма, чтобы приводить в исходное положение все подвижные детали отсчетного устройства.

Суммарное действие моментов трения, возникающих в подвижных соединениях передаточного механизма, характеризуется приведенным к оси волоска моментом трения

Приведенным моментом трения к какой-либо оси механизма называется приложенный к этой оси момент эквивалентный суммарному действию всех сил и моментов трения в передаточном механизме.

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.