Рычаг.
Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы и . Плечи этих сил равны соответственно и .
Условие равновесия рычага даётся правилом моментов: , откуда
.
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
Что такое рычаг и когда его начали применять?
Вероятно, каждый с детства знаком с этим незамысловатым механизмом. В физике рычагом называется совокупность балки (стержня, доски) и одной опоры. Служит рычаг для поднятия тяжестей либо для сообщения телам скоростей. В зависимости от положения опоры под балкой рычаг может приводить к выигрышу либо в силе, либо в перемещении грузов. Следует сказать, что рычаг не приводит к сокращению работы как физической величины, он лишь позволяет перераспределить ее выполнение удобным образом.
Систему рычагов с давних пор использует человек. Так, существуют свидетельства, что ее использовали древние египтяне при строительстве пирамид. Первое математическое описание эффекта рычага относится к III веку до нашей эры и принадлежит оно Архимеду. Современное объяснение принципа работы этого механизма с привлечением понятия момента силы возникло лишь в XVII веке, во времена становления классической механики Ньютона.
Неподвижный блок.
Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
На правом конце нити в точке закреплён груз весом . Напомним, что вес тела — это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес прило жен к точке , в которой груз крепится к нити.
К левому концу нити в точке приложена сила .
Плечо силы равно , где — радиус блока. Плечо веса равно . Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство , а во-вторых, в процессе движении груза и нити перемещение точки равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
Примеры использования систем простых механизмов
По сути, любые машины, которые нас окружают, представляют собой системы рычагов и блоков. Приведем самые известные примеры:
- печатная машинка;
- пианино;
- грузоподъемный кран;
- раскладные строительные леса;
- регулируемые кровати и столы;
- совокупность костей, суставов и мышц человека.
Если известно входное усилие в каждой из этих систем, то выходная сила может быть рассчитана с помощью последовательного применения правила рычага к каждому элементу системы.
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити .
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы «перекатывается» через точку ). Говорят ещё, что через точку проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке крепления груза к нити. Плечо силы равно .
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно . Соответственно, условием равновесия груза является равенство (что мы и видим на рис. 3: вектор в два раза короче вектора ).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) — не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
Современный взгляд на простой механизм «блок», изучаемый по учебникам физики для 7 класса
Учебники физики для 7 класса при изучении простого механизма блок по-разному трактуют получение выигрыша в силе при подъёме груза с помощью этого механизма, например: в учебнике Пёрышкина А. В. выигрыш в силе достигается с помощью колеса блока, на который действуют силы рычага, а в учебнике Генденштейна Л. Э. тот же выигрыш получают с помощью троса, на который действует сила натяжения троса. Разные учебники, разные предметы и разные силы — для получения выигрыша в силе, при подъёме груза. Поэтому целью данной статьи служит поиск предметов и сил, с помощью которых получается выигрыш в силе, при подъёме груза простым механизмом блок.
Ключевые слова: блок, двойной блок, неподвижный блок, подвижный блок, полиспаст.
Сначала ознакомимся и сравним как получают выигрыш в силе, при подъёме груза простым механизмом блок, в учебниках физики для 7 класса, для этого выдержки из текстов учебников, с одинаковыми понятиями, для наглядности разместим в таблице.
| Пёрышкин А. В. Физика. 7 класс. § 61. Применение правила равновесия рычага к блоку, стр.180–183. | Генденштейн Л. Э. Физика. 7 класс. § 24. Простые механизмы, стр.188–196. |
| «Блок представляет собой колесо с жёлобом, укреплённое в обойме. По жёлобу блока пропускают верёвку, трос или цепь. «Неподвижным блоком называют такой блок ось которого закреплена и при подъёме грузов не поднимается и не опускается (рис.177). Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис.178): ОА=ОВ=r. Такой блок не даёт выигрыша в силе (F1 = F2), но позволяет изменять направление действия силы» [1, с.181, 182]. | «Даёт ли неподвижный блок выигрыш в силе? …на рис.24.1а трос натянут силой, приложенной рыбаком к свободному концу троса. Сила натяжения троса остаётся постоянной вдоль троса, поэтому со стороны троса на груз (рыбу) действует такая же по модулю сила. Следовательно, неподвижный блок не даёт выигрыша в силе. 6.Как с помощью неподвижного блока получить выигрыш в силе? Если человек поднимает самого себя, как показано на рис.24.6, то при этом вес человека распределяется поровну на две части троса (по разные стороны блока). Поэтому человек поднимает себя прикладывая силу, которая вдвое меньше его веса», [2, с.190, 193]. |
| «Подвижный блок — это блок, ось которого поднимается и опускается вместе с грузом (рис.179). На рисунке 180 показан соответствующий ему рычаг: О — точка опоры рычага, АО — плечо силы Р и ОВ — плечо силы F. Так как плечо ОВ в 2 раза больше плеча ОА, то сила F в 2 раза меньше силы Р: F=Р/2. Таким образом, подвижный блок даёт выигрыш всиле в 2 раза» [1, с.182]. | «5. Почему подвижный блок даёт выигрыш всиле вдва раза? Рис. 24.5 При равномерном подъёме груза подвижный блок тоже движется равномерно. Значит равнодействующая всех приложенных к нему сил равна нулю. Если массой блока и трением в нём можно пренебречь, то можно считать, что к блоку приложены три силы: вес груза Р, направленный вниз, и две одинаковые силы натяжения троса F, направленные вверх. Поскольку равнодействующая этих сил равна нулю, то Р=2F, то есть вес груза в 2 раза больше силы натяжения троса. Но сила натяжения троса — это как раз и есть сила, которую прикладывают поднимая груз с помощью подвижного блока. Таким образом мы доказали, что подвижный блок даёт выигрыш в силе в 2 раза» [2, с.192]. |
| «Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.181). Неподвижный блок применяется только для удобства. Он не даёт выигрыша в силе, но изменяет направление действия силы, например позволяет поднимать груз, стоя на земле. Рис.181. Комбинация подвижных и неподвижных блоков — полиспаст» [1, с.182]. | «12.На рис 24.7 изображена система блоков. Сколько в ней подвижных блоков и сколько неподвижных? Какой выигрыш в силе даёт такая система блоков, если трением и массой блоков можно пренебречь?» [2, с.195]. Рис.24.7. Ответ на стр.240: «12.Три подвижных блока и один неподвижный; в 8 раз» [2, с.240]. |
Подведём итог ознакомления и сравнения текстов и рисунков в учебниках:
Доказательства получения выигрыша в силе в учебнике Пёрышкина А. В. проводятся на колесе блока и действующая сила — сила рычага; при подъёме груза неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе в 2 раза. О тросе, на котором висит груз на неподвижном блоке и подвижный блок с грузом, нет упоминания.
С другой стороны, в учебнике Генденштейна Л. Э. доказательства выигрыша в силе проводятся на тросу, на котором висит груз или подвижный блок с грузом и действующая сила — сила натяжения троса; при подъёме груза неподвижный блок может давать выигрыш в силе в 2 раза, а о рычаге, на колесе блока, в тексте нет упоминания.
Поиск литературы с описанием получения выигрыша в силе блоком и тросом привели к «Элементарному учебнику физики» под редакцией академика Г. С. Ландсберга, в §84. Простые машины на стр.168–175 даны описания: «простого блока, двойного блока, ворота, полиспаста и дифференциального блока». Действительно, по своей конструкции, «двойной блок даёт выигрыш в силе, при подъёме груза, за счёт разницы в длине радиусов блоков», с помощью которых происходит подъём груза, а «полиспаст — даёт выигрыш в силе, при подъёме груза, за счет верёвки, на нескольких частях которой, висит груз» [3, с.168–175]. Таким образом удалось узнать почему дают выигрыш в силе, при подъёме груза, по отдельности блок и трос (верёвка), но не удалось узнать, как блок и трос взаимодействуют между собой и передают вес груза друг другу, так как груз может быть подвешен на тросу, а трос перекинут через блок или груз может висеть на блоке, а блок висит на тросу. Выяснилось, что сила натяжения троса постоянна и действует по всей длине троса, поэтому передача веса груза тросом блоку будет в каждой точке соприкосновения троса и блока, а также передача веса груза подвешенного на блоке — тросу. Для уточнения взаимодействия блока с тросом проведём опыты по получению выигрыша в силе подвижным блоком, при подъёме груза, с использованием оборудования школьного кабинета физики: динамометры, лабораторные блоки и набор грузов в 1Н (102 г). Опыты начнём с подвижного блока, потому что имеем три разные версии получения выигрыша в силе этим блоком. Первая версия — это «Рис.180. Подвижный блок как рычаг с неравными плечами» — учебник Пёрышкина А. В., вторая «Рис.24.5… две одинаковые силы натяжения троса F», — по учебнику Генденштейна Л. Э. и наконец третья «Рис.145.Полиспаст». Подъём груза подвижной обоймой полиспаста на нескольких частях одной верёвки — согласно учебника Ландсберга Г. С.
Опыт №1. «Рис.183» [1, с.184]
Для проведения опыта № 1, получение выигрыша в силе на подвижном блоке «рычагом с неравными плечами ОАВ рис.180» по учебнику Пёрышкина А. В., на подвижном блоке «рис.183» положение 1, нарисуем рычаг с неравными плечами ОАВ, как на «рис.180», и начнём подъём груза из положения 1 в положение 2. В это же мгновение блок начинает вращение, против часовой стрелки, вокруг своей оси в точке А, а точка В — конец рычага, за который происходит подъём, выходит за пределы полуокружности, по которой трос снизу огибает подвижный блок. Точка О — точка опоры рычага, которая должна быть неподвижной, уходит вниз см. «рис.183» — положение 2, т. е. рычаг с неравными плечами ОАВ изменяется как рычаг с равными плечами (одинаковые пути проходят точки О и В).
На основе полученных данных в опыте № 1 об изменений положения рычага ОАВ на подвижном блоке при подъёме груза из положения 1 в положение 2, можно сделать вывод о том, что представление подвижного блока как рычага с неравными плечами на «рис.180», при подъёме груза, с вращением блока вокруг своей оси, соответствует рычагу с равными плечами, который не даёт выигрыша в силе, при подъёме груза [1, с.182].
Опыт № 2 начнём с крепления динамометров на концы троса, на который повесим подвижный блок с грузом весом 102 г, что соответствует силе тяжести 1 Н. Один из концов троса закрепим на подвесе, а за второй конец троса будем производить подъём груза на подвижном блоке. Перед подъёмом показания обоих динамометров по 0,5 Н, вначале подъёма показания динамометра, за который происходит подъём, изменилось до 0,6 Н, и оставалось таким во время подъёма, по окончании подъёма показания вернулись к 0,5 Н. Показания динамометра, закреплённого за неподвижный подвес не менялось во время подъёма и оставалось равным 0,5 Н. Проведём анализ результатов опыта:
- Перед подъёмом, когда груз в 1 Н (102 г) висит на подвижном блоке, вес груза распределяется на всё колесо и передаётся тросу, который снизу огибает блок, всей полуокружностью колеса.
- Перед подъёмом показания обоих динамометров по 0,5 Н, что свидетельствует о распределении веса груза в 1 Н (102 г) на две части троса (до и после блока) или о том, что сила натяжения троса равна 0,5 Н, и одинакова по всей длине троса (какая в начале, такая же и в конце троса) — оба эти утверждения верны.
Проведём сравнение анализа опыта № 2 с версиями учебников о получении выигрыша в силе в 2 раза подвижным блоком. Начнём с утверждения в учебнике Генденштейна Л. Э. «… что к блоку приложены три силы: вес груза Р, направленный вниз, и две одинаковые силы натяжения троса, направленные вверх (рис.24.5)». Точнее будет утверждение, что вес груза на «рис. 14.5» распределился на две части троса, до и после блока, так как сила натяжения троса — одна [2, с.192]. Осталось проанализировать подпись под «рис.181» из учебника Пёрышкина А. В. «Комбинация подвижных и неподвижных блоков — полиспаст». Описание устройства и получения выигрыша в силе, при подъёме груза, полиспастом дано в Элементарном учебнике физики под ред. Лансберга Г. С. где сказано: «Каждый кусок верёвки между блоками будет действовать на движущийся груз с силой Т, а все куски верёвки будут действовать с силой nT, где n — число отдельных участков верёвки, соединяющих обе части блока». Получается, что если к «рис.181» [1, с.182] применить получение выигрыша в силе «верёвкой, соединяющей обе части» полиспаста из Элементарного учебника физики Ландсберга Г. С., то описание получение выигрыша в силе подвижным блоком на «рис.179 и соответственно рис.180» будет ошибкой [1, с.182].
Проанализировав четыре учебника физики можно сделать вывод, что существующее описание получения выигрыша в силе простым механизмом блок не отвечает реальному положению дела и поэтому требует нового описания работы простого механизма блок.
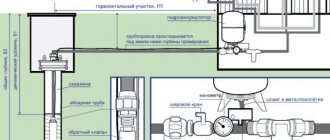
Простой грузоподъёмный механизм состоит из блока и троса (верёвки или цепи).
Блоки этого грузоподъёмного механизма подразделяются:
по конструкции на простые и сложные;
по способу подъёма груза на подвижные и неподвижные.
Знакомство с конструкцией блоков начнём с простого блока, который представляет собой колесо, вращающееся вокруг своей оси, с жёлобом по окружности для троса (верёвки, цепи) рис.1 и его можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса: ОА=ОВ=r. Такой блок не даёт выигрыша в силе, но позволяет изменять направление движение троса (верёвки, цепи).
Двойной блок состоит из двух блоков разных радиусов, жестко скреплённых между собой и насаженных на общую ось рис.2. Радиусы блоков r1 и r2 различны и при подъёме груза действуют как рычаг с неравными плечами, а выигрыш в силе будет равен отношению длин радиусов блока большего диаметра к блоку меньшего диаметра F =Р·r1/r2.
Ворот состоит из цилиндра (барабана) и прикреплённой к нему рукоятки, которая выполняет роль блока большого диаметра, Выигрыш в силе, даваемый воротом, определяется отношением радиуса окружности R, описываемой рукояткой, к радиусу цилиндра r, на который намотана верёвка F = Р·r/R.
Перейдём к способу подъёма груза блоками. Из описания конструкции все блока имеют ось, вокруг которой они вращаются. Если ось блока закреплена и при подъёме грузов не поднимается и не опускается, то такой блок называется неподвижным блоком, простой блок, двойной блок, ворот.
У подвижного блока ось поднимается и опускается вместе с грузом рис.10 и он предназначен в основном для устранения перегиба троса в месте подвеса груза.
Ознакомимся к устройством и способом подъёма груза второй частью простого грузоподъёмного механизма — это трос, верёвка или цепь. Трос свит из стальных проволочек, верёвка свита из нитей или прядей, а цепь состоит из звеньев, соединённых между собой.
Способы подвеса груза и получение выигрыша в силе, при подъёме груза, тросом:
На рис. 4 груз закреплён на одном конце троса и если поднимать груз за другой конец троса, то для подъёма этого груза потребуется сила чуть больше веса груза, так как простой блок выигрыша в силе не даёт F = Р.
На рис.5 груз рабочий поднимает самого себя за трос, который сверху огибает простой блок, на одном конце первой части троса закреплено сидение, на котором сидит рабочий, а за вторую часть троса рабочий поднимает самого себя с силой в 2 раза меньшей своего веса, потому что вес рабочего распределился на две части троса, первая — от сидения до блока, а вторая — от блока до рук рабочего F = Р/2.
На рис.6 груз поднимают двое рабочих за два троса и вес груза распределятся поровну между тросами и поэтому каждый рабочий будет поднимать груз с силой половины веса груза F = Р/2.
На рис.7 рабочие поднимают груз, который висит на двух частях одного троса и вес груза распределятся поровну между частями этого троса (как между двумя тросами) и каждый рабочий будет поднимать груз с силой равной половине веса груза F = Р/2.
На рис.8 конец троса, за который поднимал груз один из рабочих, закрепили на неподвижном подвесе, а вес груза распределился на две части троса и при подъёме груза рабочим за второй конец троса, сила, с которой рабочий будет поднимать груз, в два раза меньше веса груза F = Р/2 и подъём груза будет в 2 раза медленнее.
На рис.9 груз висит на 3 частях одного троса, один конец которого закреплён и выигрыш в силе, при подъёме груза, будет равен 3, так как вес груза распределится на три части троса F = Р/3.
Для устранения перегиба и уменьшения силы трения в месте подвеса груза устанавливается простой блок и сила необходимая для подъёма груза не изменилась, так как простой блок не даёт выигрыша в силе рис.10 и рис.11, а сам блок будет называться подвижным блоком, так как ось этого блока поднимается и опускается вместе с грузом.
Теоретически груз можно подвесить на неограниченное число частей одного троса, но практически ограничиваются шестью частями и такой грузоподъёмный механизм называется полиспаст, который состоит из неподвижной и подвижной обойм с простыми блоками, которые поочерёдно огибаются тросом, одним концом закреплённый на неподвижной обойме, а подъём груза производят за второй конец троса. Выигрыш в силе зависит от количества частей троса между неподвижной и подвижной обоймами, как правило это 6 частей троса и выигрыш в силе 6 раз.
Выводы.
В статье рассмотрены реально существующие взаимодействия между блоками и тросом при подъёме груза. Существующая практика в определении что «неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе в 2 раза» ошибочно трактовала взаимодействие троса и блока в подъёмном механизме и не отражала всего многообразия конструкции блоков, что вело к развитию односторонних ошибочных представлений о блоке. По сравнению с существующими объёмами материала для изучения простого механизма блок, объём статьи увеличился в 2 раза, но это позволило наглядно и доходчиво объяснить процессы, протекающие в простом грузоподъёмном механизме не только ученикам, но и учителям.
Литература:
- Пёрышкин, А. В. Физика, 7 кл.: учебник/ А. В. Пёрышкин.- 3-е изд., доп.- М.: Дрофа, 2014, — 224 c,: ил. ISBN 978–5-358–14436–1. § 61. Применение правила равновесия рычага к блоку, стр.181–183.
- Генденштейн, Л. Э. Физика. 7 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений/ Л. Э. Генденштен, А. Б. Кайдалов, В. Б. Кожевников; под ред. В. А. Орлова, И, И. Ройзена.- 2-е изд., испр. — М.: Мнемозина, 2010.-254 с.: ил. ISBN 978–5-346–01453–9. § 24. Простые механизмы, стр.188–196.
- Элементарный учебник физики, под редакцией академика Г. С. Ландсберга Том 1. Механика. Теплота. Молекулярная физика.- 10 изд.- М.: Наука, 1985. § 84. Простые машины, стр. 168–175.
- Громов, С. В. Физика: Учеб. для 7 кл. общеобразоват. учреждений/ С. В. Громов, Н. А. Родина.- 3-е изд. — М.: Просвещение, 2001.-158 с,:ил. ISBN-5–09–010349–6. §22. Блок, стр.55 -57.
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость — это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: «наклонная плоскость с углом «.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом . Эта сила , разумеется, направлена вдоль наклонной плоскости (рис. 5).
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что , поскольку . Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол .
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу . Но для поднятия груза на высоту большее плечо придётся опустить на , и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту над начальным положением, нам нужно пройти путь вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
Формулу расчета КПД блока полиспаста
Как всегда, КПД показывает отношение выполненной работы к затраченной. Для дальнейших расчетов давайте немного обратимся к практике.
- Первое.
При прочтении у вас, скорее всего, сразу возник вопрос о каких углах отклонения вообще идет речь? Действительно, современные полиспасты их просто не имеют. В этих углах нет никакого практического смысла. Можно смело заменить синус из формулы на единицу. - Второе.
Как уже упоминалось ранее, значение q крайне мало относительно f. В реальных условиях его опускают. Также очень малое значение имеют диаметр ручья полиспаста.
Ну, собственно, у нас остается только сила трения блока полиспаста о его втулку. Таким образом, основное значение при выборе полиспаста имеет качество материалов, из которых он изготовлен, а вернее материалы втулки.
При расчетах используются следующие величины КПД блока полиспаста:
- 100% — недостижимый идеал;
- 97% — среднее значение при использовании бронзовых втулок в подшипниках качения;
- 95% — средние значение при использовании подшипников скольжения;
- 93% и меньше — сильно запыленные места, сильно повышенная температура или агрессивные среды использования.
Не забываем, что мы до сих пор рассматриваем один единственный ролик, а он у нас не один и не два.