Внутренние усилия при растяжении и сжатии
При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие. На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.
Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.
Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.
Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:
U=W=FΔl/2=N²l/(2EA)
Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.
Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.
Сопротивление сжатию
Различают три основных направления усилий при сжатии древесины: 1) вдоль волокон, 2) поперек волокон в радиальном направлении и 3) поперек волокон в тангентальном направлении (рис. 21). Величина временного сопротивления сжатию в остальных направлениях принимает промежуточные значения между значениями, соответствующими основным направлениям.
Сопротивление сжатию вдоль волокон
Сравнительно высокое временное сопротивление древесины при сжатии вдоль волокон обусловливает широкое применение сжатых стоек в различных сооружениях.
Предел пропорциональности при сжатии вдоль волокон весьма высок. По данным Мадисоновской лаборатории (США), отношение предела пропорциональности к временному сопротивлению составляет:
- для хвойных пород 0,78
- для мягких лиственных 0,77
- для твердых лиственных 0,66
С уменьшением влажности сопротивление сжатию увеличивается.
Кривая изменения временного сопротивления сжатию у ели в зависимости от влажности показана на рис. 22. Из нее видно, что наиболее сильное возрастание временного сопротивления происходит в пределах от 15% до абсолютно сухого состояния.
Рис. 22. Диаграмма зависимости сопротивления древесины ели сжатию от влажности.
Для определения зависимости между влажностью и временным сопротивлением имеется эмпирическая формула:
σ15 = σW[1+ α(W-15)],
где σ15-временное сопротивление при 15% влажности, σW — временное сопротивление при влажности W, W — влажность древесины в %, α — коэффициент, зависящий от породы древесины.
Коэффициенты α для разных пород приведены в табл. 23.
Таблица 23 – Коэффициент а, определяющий зависимость временного сопротивления сжатию вдоль волокон от влажности
| Порода дерева | Коэффициент α |
| Береза | 0,045 |
| Дуб | 0,040 |
| Клен | 0,040 |
| Лиственница сибирская | 0,050 |
| Сосна | 0,050 |
| Ясень | 0,050 |
Для сосны, ели аянской, ели обыкновенной, пихты кавказской и дельта-древесины зависимость между влажностью и временным сопротивлением сжатию вдоль волокон более точно определяется по формуле:
σ15 = KσW
где К — переводный коэффициент (приведен в табл. 24).
Временное сопротивление сжатию зависит и от объемного веса древесины. Эта зависимость может быть выражена в виде уравнения прямой с параметрами, характерными для различных пород (табл. 25).
Таблица 24 Коэффициент К для пересчета временного сопротивления сжатию вдоль волокон древесины при различных значениях влажности в зависимости от σ15
| Влажность% | 0 | 1/4 % | 1/2 % | 3/4 % |
| 1. Для сосны | ||||
| 8 | 0,683 | 0,693 | 0,704 | 0,714 |
| 9 | 0,725 | 0,735 | 0,746 | 0,757 |
| 10 | 0,767 | 0,778 | 0,789 | 0,800 |
| 11 | 0,811 | 0,823 | 0,834 | 0,845 |
| 12 | 0,857 | 0,868 | 0,880 | 0,891 |
| 13 | 0,903 | 0,915 | 0,927 | 0,939 |
| 14 | 0,951 | 0,963 | 0,975 | 0,988 |
| 15 | 1,000 | 1,013 | 1,025 | 1,038 |
| 16 | 1,050 | 1,063 | 1,076 | 1,089 |
| 17 | 1,102 | 1,115 | 1,128 | 1,141 |
| 18 | 1,155 | 1,168 | 1,182 | 1,195 |
| 19 | 1,209 | 1,223 | 1,236 | 1,250 |
| 20 | 1,264 | — | — | — |
| 2. Для ели обыкновенной и аянской | ||||
| 8 | 0,749 | 0,757 | 0,764 | 0,771 |
| 9 | 0,779 | 0,786 | 0,794 | 0,802 |
| 10 | 0,810 | 0,818 | 0,826 | 0,835 |
| 11 | 0,843 | 0,852 | 0,860 | 0,869 |
| 12 | 0,878 | 0,888 | 0,897 | 0,906 |
| 13 | 0,916 | 0,926 | 0,936 | 0,946 |
| 14 | 0,956 | 0,967 | 0,978 | 0,989 |
| 15 | 1,000 | 1,012 | 1,023 | 1,035 |
| 16 | 1,047 | 1,059 | 1,072 | 1,085 |
| 17 | 1,098 | 1,111 | 1,125 | 1,138 |
| 18 | 1,152 | 1,167 | 1,182 | 1,197 |
| 19 | 1,212 | 1,229 | 1,245 | 1,261 |
| 20 | 1,277 | 1,295 | 1,313 | 1,330 |
| 3. Для пихты кавказской | ||||
| 8 | 0,724 | 0,733 | 0,741 | 0,750 |
| 9 | 0,760 | 0,769 | 0,778 | 0,788 |
| 10 | 0,798 | 0,807 | 0,818 | 0,828 |
| 11 | 0,838 | 0,848 | 0,858 | 0,868 |
| 12 | 0,879 | 0,889 | 0,899 | 0,909 |
| 13 | 0,920 | 0,930 | 0,940 | 0,950 |
| 14 | 0,960 | 0,970 | 0,980 | 0,990 |
| 15 | 1,000 | 1,010 | 1,019 | 1,029 |
| 16 | 1,038 | 1,047 | 1,056 | 1,065 |
| 17 | 1,073 | 1,081 | 1,090 | 1,098 |
| 18 | 1,105 | 1,113 | 1,120 | 1,12Т |
| 19 | 1,133 | 1,140 | 1,142 | 1,152 |
| 20 | 1,157 | — | — | — |
| 4. Для дельта-древесины | ||||
| 3 | 0,812 | 0,835 | 0,857 | 0,880 |
| 4 | 0,903 | 0,927 | 0,951 | 0,975 |
| 5 | 1,000 | 1,025 | 1,049 | 1,074 |
| 6 | 1,098 | 1,122 | 1,146 | 1,170 |
| 7 | 1,192 | 1,214 | 1,235 | 1,255 |
| 8 | 1,274 | — | — | — |
Таблица 25 Уравнения зависимости между объемным весом и временным сопротивлением сжатию (по Ванину)
| Порода дерева | Уравнение зависимости |
| Береза | σсж15=1700γ15-555 |
| Дуб | σсж15=1285γ15-380 |
| Ель | σсж15= 1000γ15-70 |
| Клен | σсж15=1200γ15-335 |
| Лиственница сибирская | σсж155=740γ15+21 |
| Сосна | σсж15=1250γ15+25 |
| Ясень | σсж15=1400γ15+25 |
Наклон волокон по отношению к направлению действующих усилий оказывает большое влияние на сопротивление сжатию (рис. 23). Заметное падение сопротивления начинается при угле между направлением силы и направлением волокон и 7—8°. При дальнейшем увеличении этого угла примерно до 45° сопротивление резко падает, после чего кривая сопротивления снижается более медленно.
Рис. 23. Диаграмма зависимости сопротивления сжатию от наклона волокон. 1—в тангентальной плоскости, 2 — в радиальной плоскости.
Рис. 24. Характер разрушения древесины при сжатии.
В радиальной плоскости линия разрушения от сжатия вдоль волокон обычно направлена перпендикулярно волокнам, а в тангентальной плоскости эта линия направлена под углом к направлению волокон (рис. 24). Сырая древесина при разрушении от сжатия дает менее шероховатую и иглистую поверхность, чем сухая, в которой встречаются отщепы и откалывание волокон.
Сопротивление сжатию вдоль волокон примерно в два раза меньше сопротивления растяжению в том же направлении.
Сопротивление сжатию поперек волокон
Сопротивление древесины сжатию поперек волокон составляет менее трет» сопротивления сжатию вдоль волокон для древесины хвойных пород (27%) и менее половины (40%) для древесины лиственных пород.
Среднее соотношение между сопротивлением сжатию вдоль волокон σсж вд и поперек волокон σсж п может быть выражено соотношением σсж п = 0,36 σсж вд
Предел пропорциональности при сжатии поперек волокон очень низок у хвойных пород (около 35% от разрушающей нагрузки у сосны) и довольно высок у лиственных пород (70% от разрушающей нагрузки для дуба и березы).
Сопротивление сжатию поперек волокон в радиальном и в тангентальном направлениях зависит в лиственных породах от величины сердцевинных лучей и от неоднородности строения годовых слоев. В древесине пород, где сердцевинные лучи хорошо развиты (дуб, бук, клен, береза), сопротивление радиальному сжатию в среднем в 1,5 раза выше сопротивления тангентальному сжатию. Древесине лиственных пород со слабо Развитыми сердцевинными лучами сопротивления .сжатию в радиальном и тангентальном направлениях примерно одинаковы.
У хвойных пород наблюдается обратное явление: сопротивление сжатию в тангентальном направлении в 1,5 раза выше сопротивления в радиальном направлении.
Влияние влажности на сопротивление древесины сжатию поперек волокон также довольно значительно. Поправочный коэффициент для сосны при сжатии в тангентальном направлении составляет 4,5% и в радиальном направлении 3,5% на 1% влажности.
Для лиственных парод поправочный коэффициент значительно выше и . в среднем принимается в 6%. В том и другом случае повышенная влажность понижает сопротивление сжатию.
- перетяжка мебели своими руками
Напряжения при растяжении сжатии
Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т.к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:
Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.
Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:
Δl=Nl/EA
Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).
В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии.
В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения. Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.
Сжатие хрупкого материала
Цилиндрический образец чугуна (ho/do=1,5) после обмера устанавливается между плитами пресса и подвергается статическому нагружению. Диаграмма сжатия при этом будет иметь вид, показанный на рис. 2. Нетрудно заметить, что на диаграмме сжатия отсутствует прямолинейный участок. Разрушение происходит внезапно при нагрузке Рmах с появлением ряда наклонных трещин, направленных примерно под углом 45° к оси образца. Такой характер разрушения объясняется действием касательных напряжений, возникающих в наклонных площадках при сжатии.
Рис.2 Диаграмма сжатия и характер разрушения образцов из чугуна
Таким образом, при сжатии хрупких материалов и при их растяжении можно определить лишь предел прочности
Различие между диаграммами сжатия и растяжения чугуна заключается лишь в том, что нагрузка, соответствующая пределу прочности при сжатии, в 3-5 раз превышает нагрузку, соответствующую пределу прочности при растяжении, и соответственно (σв)с > (σв)р, т.е. чугун лучше сопротивляется сжатию, чем растяжению.
Характер деформации образца и причины его разрушения для хрупкого материала во многом зависят от влияния сил трения между образцом и опорными поверхностями машины. Путем периодической парафиновой смазки торцов образца в процессе испытания можно практически полностью устранить силы трения. При этом образец в течение всего испытания не принимает бочкообразную форму, остается цилиндрическим и разрушается по плоскостям, параллельным диаметральной плоскости образца из-за недопустимо больших растягивающих деформаций.
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
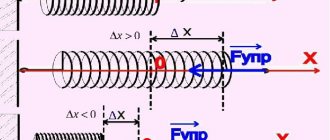
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.