Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.
Балки в доме
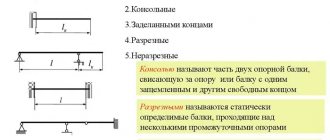
При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.
Виды балок
Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.
Деревянные
Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.
Деревянные перекрытия
Для расчета максимального прогиба следует учитывать:
- Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
- Форма поперечного сечения и другие геометрические характеристики.
- Различные виды нагрузки на материал.
Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.
Конструкции из древесины хвойных пород
Стальные
Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.
Стальные перекрытия
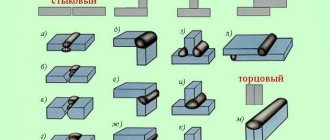
Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:
- электросварка;
- заклепки;
- болты, винты и другие виды резьбовых соединений.
Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.
Для проведения расчета балки на прогиб может помочь видео:
Прогибы балок
Как и в случае осевого нагружения, в изгибе будем допускать лишь малые деформации. Напомню, что для определения удлинений при растяжении за длину берётся исходная недеформированная длина, несмотря на тот факт, что при равномерном приложении нагрузки с каждым её увеличением увеличивается и исходная длина в каждый момент времени. То же самое и в изгибе – принимаем, что прогибы балки не влияют на её работу под нагрузкой и итоговая нагрузка прикладывается к недеформированной балке. На основе этого допущения выведем формулу для расчёта прогибов.
Имеющейся балочной теории достаточно лишь для того, чтобы определять прогибы для балок, где имеется участок чистого изгиба, на котором постоянен радиус кривизны. Его можно определить из формулы:
Максимальный прогиб в таком случае определяется как высота сегмента окружности радиуса r.
Однако в общем случае изгиба имеется поперечная сила Q, и, как следствие этого, меняется изгибающий момент M. И если балка имеет постоянное сечение по длине, то тогда меняется и радиус кривизны.
Чем больше момент в сечении, тем меньше будет радиус кривизны.
Важно упомянуть, что при общем случае нагружения на балку будет действовать поперечная сила, которая также может оказывать влияние на прогибы. Хотя в длинных балках, где успевает «набежать» достаточно большой изгибающий момент, её влияние на прогибы становится крайне незначительным, в коротких балках обычно учитывают влияние сдвиговых деформаций, хотя и для их учёта требуется более сложная техника расчёта. В пределах данного курса мы ограничимся определением прогибов балок только от изгибающих моментов, действующих их сечениях.
Для того, чтобы при определении прогибов балок учитывать изменение изгибающего момента и, следовательно, радиусов кривизны, нужно получить зависимость кривизны кривой (а, следовательно, и момента M) от координаты x и y.
В курсе математического анализа даётся вывод формулы для кривизны плоской кривой:
Для заинтересованных ниже приводится вывод данной формулы.
Пусть имеется график функции y(x):
Отметим точку на графике m и проведём касательную к графику в этой точке. Угол между касательной и осью x обозначим как α:
На некотором расстоянии ∆s от точки m на графике обозначим точку m1, в которой также проведём касательную к графику. Угол между касательной и осью x обозначим как α–∆α:
Приращение по иксу – dx, приращение по игреку – dy:
С физической точки зрения кривизна – это:
Нужно избавиться от α и от s, выразив их через координаты y и x:
По определению производной:
Получим:
Рассмотрим второй множитель:
ds можно преобразовать по теореме Пифагора:
Подставим в итоговое выражение:
С геометрической точки зрения кривизна равняется:
Получившееся уравнение связывает радиус кривизны с координатами икс (сечение балки) и игрек (её прогиб).
Используя выведенные ранее зависимости, получим:
Это уравнение называют дифференциальным уравнением упругой оси. Оно нелинейно и пользоваться им для решения практических задач крайне неудобно. Однако можно заметить, что в отношении dy/dx (dy/dx – это наклон касательной к кривой в какой-либо точке) dy весьма мало для случаев малых прогибов относительно dx (малых – относительно длины балки). И уж тем более квадрат этого отношения стремится к нулю. Фактически, это обращает знаменатель в единицу и значительно упрощает выражение:
Удобнее записать так:
Для получения прогибов, это уравнение следует дважды проинтегрировать по dx.
Для наглядности рассмотрим пример. Пусть имеется шарнирно опёртая балка с равномерно распределённой нагрузкой:
На самом деле, такое нагружение справедливо для каждой шарнирно опёртой балки, ведь никто не отменял земную гравитацию. Ну и нам хотелось бы определить прогибы этой балки, как наибольший, так и в любой желаемой нами точке.
Для начала определим опорные реакции:
Чтобы определить прогибы, нам нужно знать модуль Юнга материала E, момент инерции сечения Iz (он не должен меняться по длине) и зависимость изгибающего момента по длине. Допустим, у нас есть свойства материала и характеристики сечения. Теперь нужно получить зависимость M(x).
Проинтегрируем по dx:
Здесь C – постоянная интегрирования. Её можно определить из граничных условий:
- При x=0, прогиб балки y=0
- При x=L, прогиб балки y=0
Данные граничные условия нельзя использовать в полученном выше уравнении, так как оно для углов поворота dy/dx, а необходимо уравнение прогибов y(x). Для получения уравнения прогибов проинтегрируем ещё раз по dx:
Здесь D – ещё одна постоянная интегрирования. Так как полученное уравнение является функцией прогибов балки, то можно использовать имеющиеся граничные условия.
Первое условие:
Второе условие:
Итого:
Уравнение для углов поворота:
Уравнение для прогибов:
Решим задачу отыскания места наибольшего прогиба и величину этого прогиба. В месте наибольшего прогиба производная функции прогиба будет равна нулю. Т.е. надо полученное выражение для dy/dx приравнять к нулю:
Уравнение имеет три корня:
Второй корень при какой бы то ни было длине балки L получается отрицательным; третий корень при какой бы то ни было длине L получается большим, чем длина балки. Остаётся только первый корень L/2, значит наибольший прогиб будет в середине пролёта, что для данного примера достаточно очевидно.
Место наибольшего прогиба также можно определить, построив непосредственно график функции прогибов. Это гораздо легче способа с решением кубического уравнения.
Для этого рассмотрим частный случай. Пусть:
Для построения графика функции прогибов воспользуемся программой MS Excel. Прежде чем это сделать, необходимо ещё раз проверить свои вычисления, так как при решении громоздких уравнений легко допустить ошибку, что может привести к ошибочным результатам.
После построения получим:
Из графика можно определить как место наибольшего прогиба, так и его величину, а также прогибы в любых интересующих точках.
Наибольший прогиб:
В качестве второго примера решим следующую задачу. Необходимо найти прогибы шарнирно опёртой балки при действии распределённой силы q и сосредоточенной силы P, если балка сделана из стали с модулем упругости E = 200 000 МПа, и имеет прямоугольное поперечное сечение с размерами B и H (размеры будут даны позже, сначала задача будет решена в общем виде).
Необходимо найти прогибы шарнирно опёртой балки при действии распределённой силы q и сосредоточенной силы P, если балка сделана из стали с модулем упругости 200 000 МПа, и имеет прямоугольное поперечное сечение с размерами B и H.
На балку действует два вида нагрузок: распределённая и сосредоточенная. Допустим, что последовательность приложения этих нагрузок не оказывает влияния на работу балки, т.е. результат действия суммы всех сил тот же, что и сумма результатов действия всех сил по отдельности. Это так называемый принцип независимости действия сил. Он вполне согласуется с тем, что происходит в реальности. Тогда данная задача распадается на три подзадачи:
- Определение прогибов шарнирно-опёртой балки при распределённой нагрузке;
- Определение прогибов шарнирно-опёртой балки при сосредоточенной нагрузке;
- Суммирование прогибов.
Первая подзадача уже решена и уравнение прогибов имеет следующий вид:
Решим вторую подзадачу:
Опоры заменяются своими реакциями на балку:
Из уравнений статики получается, что:
В отличие от случая распределённой нагрузки, здесь имеется два участка, на которых функция изгибающего момента меняет свой вид.
Первый участок:
Имея дифференциальное уравнение упругой оси
Получим:
Проинтегрируем по dx и получим уравнение углов поворота для первого участка:
Ещё раз проинтегрируем по dx и получим уравнение прогибов для первого участка:
Теперь рассмотрим второй участок:
Проинтегрируем по dx и получим уравнение углов поворота для второго участка:
Ещё раз проинтегрируем по dx и получим уравнение прогибов для второго участка:
Получилось четыре неизвестных постоянных интегрирования: C1, D1, C2, D2.
Для их определения имеются следующие граничные условия:
- x=0, y=0 (первый участок)
- x=a, dy/dx (1) = dy/dx (2) (для обоих участков)
- x=a, y (1) = y (2) (для обоих участков)
- x=L, y=0 (второй участок)
Для определения зависимости между соответственными постоянными интегрирования на обоих участках, используем условия, что угол поворота и прогиб в месте приложения силы P равны для обоих участков:
Для определения D используем условие x=0, y=0 для уравнения прогибов первого участка:
Для определения C используем условие x=L, y=0 для уравнения прогибов второго участка:
Итого получим:
При
Для построения графика прогибов зададимся значениями:
Момент инерции сечения относительно изгибаемой оси:
Для построения графиков прогибов использована программа MS Excel.
Прогибы балки от сосредоточенной нагрузки:
Прогибы балки от распределённой нагрузки:
Суммарные прогибы:
Применение принципа суперпозиции для решения задач (отыскания прогибов и т.д.) удобно лишь тогда, когда у вас уже имеются готовые решения для отдельных нагружений и остаётся только просуммировать результат. В остальном, в большинстве случаев бывает проще посчитать балку сразу с учётом всех нагрузок.
Прочность и жесткость балки
Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.
Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.
Существует два основных метода расчета прочности и жесткости:
- Простой. При использовании данного метода применяется увеличительный коэффициент.
- Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.
Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.
Расчет балок на прогиб
Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
- Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.
Расчет на жесткость
Для расчета прочности балки на изгиб применяется формула:
Где:
M – максимальный момент, который возникает в балке;
Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.
Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.
γc представляет собой коэффициент условий работы, который является табличной величиной.
Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:
- Составление расчетной схемы объекта.
- Расчет размеров балки и ее сечения.
- Вычисление максимальной нагрузки, которая воздействует на балку.
- Определение точки приложения максимальной нагрузки.
- Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
- Вычисление значения жесткости или максимально прогиба балки.
Чтобы составить расчетную схему, потребуются такие данные:
- размеры балки, длину консолей и пролет между ними;
- размер и форму поперечного сечения;
- особенности нагрузки на конструкцию и точно ее приложения;
- материал и его свойства.
Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.
Расчет балки на прогиб – формулы и инструкция
В инженерных и инженерно-строительных науках (сопротивление материалов, строительная механика, теория прочности), под балкой понимается элемент несущей конструкции, воспринимающаяся преимущественно на изгибные нагрузки, и имеющая различные формы поперечного сечения.
- Основные положения расчетных методик ↓
- Алгоритм расчета на жесткость ↓
- Определение моментов инерции и сопротивления сечения ↓
- Определение максимальной нагрузки и прогиба ↓
- Особенности расчета на прогиб ↓
- Разновидности балок, применяемых в строительстве ↓
- Деревянные ↓
- Стальные ↓
Конечно, в реальном строительстве, балочные конструкции подвержены и другим видам нагружения (ветровой нагрузке, вибрации, знакопеременному нагружения), однако основной расчет горизонтальных, многоопертых и жесткозакрепленных балок проводится на действие или поперечной, или приведенной к ней эквивалентной нагрузке.
Расчетная схема рассматривает балку как жесткозакрепленный стержень или как стержень, установленный на двух опорах. При наличии 3 и более опор, стержневая система считается статически неопределимой и расчет на прогиб как всей конструкции, так и ее отдельных элементов, значительно усложняется.
При этом, основное нагружение рассматривается как сумма сил, действующая в направлении перпендикулярному сечению. Целью расчета на прогиб является определение максимального прогиба (деформации) который не должен превышать предельных значений и характеризует жесткость как отдельного элемента (так и всей связанной с ней строительной конструкции.
Определение максимальной нагрузки и прогиба
Для точного определения прогиба балки, лучше всего применять данную формулу:
Где:
q является равномерно-распределенной нагрузкой;
E – модуль упругости, который является табличной величиной;
l – длина;
I – момент инерции сечения.
Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.
Как вычислить вспомогательные величины
Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):
Wn(требуемое) = М мах / (Ry * Уc)
Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:
f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦], где
- L – продольный размер, в метрах
- E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
- J – момент инерции по сечению
- qn – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м
Показатель J рассчитывается так:
J = b * h3 / 12
Обозначения:
- b – диаметр сечений
- h – вертикальный размер сечения
Примером для сечений, величиной 15 на 20 сантиметров:
J = 0,15 * (0,2)3 / 12 = 10 000 см4 или 0,0001 м4
Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).
Особенности расчета на прогиб
Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:
- Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
- Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
- Варианты нагружения консольного стержня, который закреплен жестко.
- Действие на конструкцию сложной нагрузки.
Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.